��Ŀ����
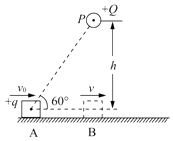
����Ŀ����ͼ��ʾ��һ����ΪmA=1kg��С��A��vB=1m/s���ٶ��ع⻬ˮƽ�������������˶���ijʱ����һ����ΪmB=2kg�����B��vB=2m/s���ٶȴ������һ���С����ʹС��Aǡ��û������ǰ�����ϰ����֪С��A�ϱ���ˮƽ���㹻�������Bû�ܻ���С�������B��С��A��Ķ�Ħ������Ϊ0.2���������ٶ�g=10m/s2 �� ��
�����B����С��Aʱ��С��A���ϰ���ľ��룻
�����B��С��A�����С��A���еľ��룮![]()
���𰸡��⣺�������B����С��Aʱ��С��A���ϰ���ľ���ΪL�䣬����С��A��Ӧ�ö��ܶ����ɵã�
����mgL��=0�� ![]() mAvA2
mAvA2
�������ݽ�ã�L��=0.125m��
��������С��������Ծ�ֹʱ�ٶ�Ϊv����������С����ɵ�ϵͳ�������غ㣬�������˶�����Ϊ���������У�
mBvB��mAvA=��mA+mB��v
�����B��С��A�ϻ��еľ���ΪL����ϵͳ�����غ�ɵã�
��mBgL= ![]() mAvA2+
mAvA2+ ![]() mBvB2��
mBvB2�� ![]() ��mA+mB��v2
��mA+mB��v2
�������ݽ�ã�L=0.75m��
�𣺢����B����С��Aʱ��С��A���ϰ���ľ�����0.125m��
��С��A�ij��Ⱦ�����0.75m��
�����������A���˶����̣�A���������ȼ����˶���ʹС��Aǡ��û������ǰ�����ϰ��˵�������ϰ���λ���ٶȸպü���0��
A�����������ȼ��٣�Bһֱ���ȼ��٣������ٶ���ͬʱ�����٣�����ͨ�������غ㶨��������յĹ�ͬ�ٶȣ�
���B���ոպ�û�ܻ���С������ʾB�ѵ���С�����Ҷˣ����������غ㣬ϵͳ�Ķ��ܵ���ʧת����A��B�Ħ�����������ܣ��г���ʽ������⣮
�����㾫����������Ҫ�����˶��ܶ������ۺ�Ӧ�úͶ����غ㶨�ɵ����֪ʶ�㣬��Ҫ����Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ������غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��������ȷ�����⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�