题目内容
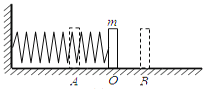
【题目】如图所示,在光滑水平面上放置一个质量M=2kg的长木板A,可视为质点的物块B放在木板A的最左端,其质量m=1kg.已知A、B间的动摩擦因数为μ=0.2.开始时A、B均处于静止状态.某时刻B突然获得水平向右的初速度v0=6m/s,g取10m/s2.
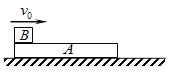
(1)计算物块B获得速度v0后,开始向右运动时加速度的大小;
(2)若物块B恰好不从A的右端滑出,计算木板A的长度L;
(3)在(2)情形下,当物块B运动到木板A的右端时,立即在A上施加一个水平向右的拉力F=12N(图中未画出),计算物块B离开木板A时的速度.
【答案】(1)2 m/s2 ;(2)6 m; (3)6 m/s
【解析】
(1)根据牛顿第二定律求解物块B的加速度;(2)物块B恰好不从A的右端滑出,则当两者速度相等时,B恰好滑到A的右端,结合位移关系求解木板A的长度L;(3).在A上施加拉力F后,A继续向右加速,A的速度将大于B,B受到的摩擦力反向,也改为向右加速,根据牛顿第二定律求解加速度,结合位移关系求解物块B离开木板A时的速度.
(1)根据牛顿第二定律,物块B开始向右运动时
μmg=maB
解得aB=2 m/s2
(2)开始运动后,B做匀减速运动,A做匀加速运动,当两者速度相等时,B恰好滑到A的右端.设此时它们的共同速度为v,经历的时间为t.
由速度关系有v=aAt=v0-aBt
由位移关系有![]()
另有μmg=MaA
联立解得:v=2 m/s,L=6 m
(3)在A上施加拉力F后,A继续向右加速,A的速度将大于B,B受到的摩擦力反向,也改为向右加速.由牛顿第二定律
对A有:F–μmg=Ma′A
对B有:μ1mg=ma′B
联立解得:a′A=5 m/s2,a′B=2 m/s2
由于a′A> a′B,虽然两者都向右加速,但B相对于A向左运动,设经过时间t′,物块B从左端离开A.
由位移关系有:![]()
解得t′=2s
所以B离开A时的速度 ![]() m/s
m/s

 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案