题目内容
9.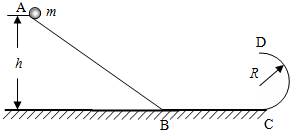 如图所示,斜面AB、水平轨道BC和半圆形轨道CD平滑连接,AB、BC和CD处于同一平面内,CD的半径为R=0.4m.质量m=0.5kg的小球(可看做质点)从A点静止开始下滑,恰能到达D点.不计一切摩擦,g取10m/s2,求:
如图所示,斜面AB、水平轨道BC和半圆形轨道CD平滑连接,AB、BC和CD处于同一平面内,CD的半径为R=0.4m.质量m=0.5kg的小球(可看做质点)从A点静止开始下滑,恰能到达D点.不计一切摩擦,g取10m/s2,求:(1)小球通过半圆形轨道最低点C时,轨道对小球的支持力;
(2)斜面的最高点A离地面的高度h.
分析 (1)根据牛顿第二定律求出D点的速度,结合机械能守恒定律求出C点的速度,通过牛顿第二定律求出轨道对小球的支持力.
(2)根据机械能守恒定律求出斜面的最高点A离地面的高度h.
解答 解:(1)小球恰好到达D点,根据牛顿第二定律得:$mg=m\frac{{v{\;}_D^2}}{R}$
解得:vD=$\sqrt{gR}=\sqrt{10×0.4}$m/s=2m/s
根据机械能守恒有:$\frac{1}{2}mv_D^2+mg2R=\frac{1}{2}mv_c^2$…①
根据牛顿第二定律得:${F_支}-mg=m\frac{{v{\;}_c^2}}{R}$…②
联立①②解得:F支=255N.
(2)根据机械能守恒有:mgh=$\frac{1}{2}m{{v}_{C}}^{2}$,
联立代入数据解得:h=1m.
答:(1)小球通过半圆形轨道最低点C时,轨道对小球的支持力为255N;
(2)斜面的最高点A离地面的高度h为1m.
点评 本题考查了机械能守恒与曲线运动的综合,知道圆周运动向心力的来源是解决本题的关键,难度不大.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
20.交流发电机工作时产生的感应电动势的最大值为Em,周期为T;若使其电枢的转速提高一倍,其它条件不变,其电动势的最大值Em′和周期T′为( )
| A. | Em′=Em | B. | Em′=2Em | C. | T′=T | D. | T′=2T |
14.关于经典力学和相对论、量子力学,下列说法正确的是( )
| A. | 不论是对宏观物体,还是微观粒子,经典力学和量子力学都是适用的 | |
| B. | 经典力学适用于低速运动的物体,相对论适用于高速运动的物体 | |
| C. | 经典力学适用于宏观物体的运动,量子力学适用于微观粒子的运动 | |
| D. | 相对论与量子力学否定了经典力学理论 |
1.高三某同学对自己在本学期学校体检后的一些数据在单位上作了一些转化,其中部分数据在如下选项中给出,在他给出的数据中,属于国际单位制中基本单位的是( )
| A. | 体重G=637N | B. | 质量m=65kg | C. | 身高H=178cm | D. | 血压115/75mmHg |
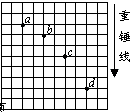 “研究平抛运动”实验中,在印有小方格纸上记下小球在空中运动的一系列位置 a、b、c、d,如图所示.已知图中小方格边长的实际长度为L,则小球水平抛出时的初速度v0=$2\sqrt{gL}$(用重力加速度g、边长L表示).
“研究平抛运动”实验中,在印有小方格纸上记下小球在空中运动的一系列位置 a、b、c、d,如图所示.已知图中小方格边长的实际长度为L,则小球水平抛出时的初速度v0=$2\sqrt{gL}$(用重力加速度g、边长L表示).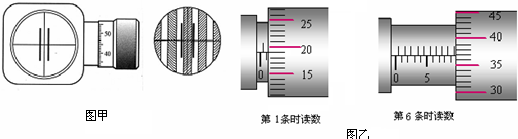
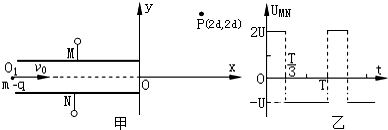
 如图甲,光滑的水平面上有三个滑块a、b、c;ma=1kg,mb=3kg;b、c被一根轻质弹簧连接在一起,处于静止状态;在t=0时,滑块a突然以水平向右的速度与b正碰,并瞬间粘合成一个物体(记为d);此后运动过程中弹簧始终处于弹性限度内,d的速度随时间做周期性变化,如图乙.则:
如图甲,光滑的水平面上有三个滑块a、b、c;ma=1kg,mb=3kg;b、c被一根轻质弹簧连接在一起,处于静止状态;在t=0时,滑块a突然以水平向右的速度与b正碰,并瞬间粘合成一个物体(记为d);此后运动过程中弹簧始终处于弹性限度内,d的速度随时间做周期性变化,如图乙.则: