题目内容
18.对太阳系的行星,由公式v=$\frac{2πr}{T}$,F=m$\frac{v^2}{r}$,$\frac{{r}^{3}}{{T}^{2}}$=k可以得到F=$\frac{4{π}^{2}km}{{r}^{2}}$,这个公式表明太阳对不同行星的引力,与行星的质量成正比,与行星和太阳距离的二次方成反比.分析 行星绕太阳做圆周运动的向心力由太阳对行星的万有引力提供,根据万有引力公式及向心力公式分析答题.
解答 解:对太阳系的行星,由公式v=$\frac{2πr}{T}$得:
F=$m\frac{{v}^{2}}{r}=\frac{4{π}^{2}mr}{{T}^{2}}$,
而$\frac{{r}^{3}}{{T}^{2}}=k$
可以得到F=$\frac{4{π}^{2}km}{{r}^{2}}$,
这个公式表明太阳对不同行星的引力,与行星的质量成正比,与行星和太阳距离的二次方成反比.
故答案为:$\frac{4{π}^{2}km}{{r}^{2}}$,行星的质量,行星和太阳距离的二次方
点评 解决本题的点关键知道万有引力提供行星做圆周运动的向心力,万有引力的大小与行星到太阳的距离的平方成反比.

练习册系列答案
相关题目
8.当物体的重力做正功时,物体的( )
| A. | 重力势能一定增加,动能一定减少 | |
| B. | 重力势能一定减少,动能一定增加 | |
| C. | 重力势能一定减少,动能不一定增加 | |
| D. | 重力势能不一定减少,动能不一定增加 |
6.某实验小组为了研究小车的运动速度随时间的变化规律,实验桌上已准备了带滑轮的长木板,小车,细线,钩码,纸带,其它器材需要自己选择,请你从图1中选出你认为需要的器材完成实验.
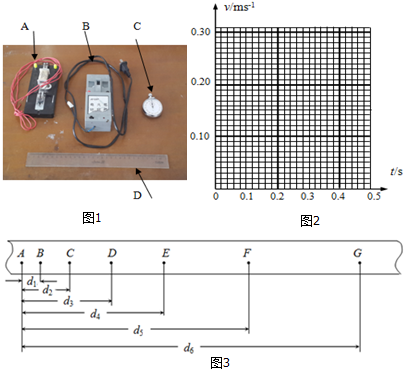
(1)你选择的器材是B、D(请填写字母);
(2)某同学选择好器材后,经过实验得到一条用打点计时器打下的纸带如图2所示,并在其上取A、B、C、D、E、F、G等7个计数点,每相邻两个计数点间还有4个点,图中没有画出,打点计时器接周期为T的交流电源.他经过测量和计算得到打点计时器打下B、C、D、E、F各点时小车的瞬时速度,记录在下面的表格中.
计算打点计时器打下F点时小车的瞬时速度的公式为VF=$\frac{{d}_{6}-{d}_{4}}{10T}$;
(3)根据上面得到的数据,以A点对应的时刻为t=0时刻,在图3的坐标纸上作出小车的速度随时间变化的v-t图线;
(4)由v-t图线求得小车的加速度a=0.42m/s2(计算结果保二位有效数字)

(1)你选择的器材是B、D(请填写字母);
(2)某同学选择好器材后,经过实验得到一条用打点计时器打下的纸带如图2所示,并在其上取A、B、C、D、E、F、G等7个计数点,每相邻两个计数点间还有4个点,图中没有画出,打点计时器接周期为T的交流电源.他经过测量和计算得到打点计时器打下B、C、D、E、F各点时小车的瞬时速度,记录在下面的表格中.
| 对应点 | B | C | D | E | F |
| 速度/ms-1 | 0.122 | 0.164 | 0.205 | 0.250 | 0.289 |
(3)根据上面得到的数据,以A点对应的时刻为t=0时刻,在图3的坐标纸上作出小车的速度随时间变化的v-t图线;

(4)由v-t图线求得小车的加速度a=0.42m/s2(计算结果保二位有效数字)
13.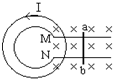 如图所示,两同心金属圆环共面,其中大闭合圆环与导轨绝缘,小圆环的开口端点与导轨相连,平行导轨处在水平面内,磁场方向竖直向下,金属棒ab与导轨接触良好,为使大圆环中产生图示电流,则ab应当( )
如图所示,两同心金属圆环共面,其中大闭合圆环与导轨绝缘,小圆环的开口端点与导轨相连,平行导轨处在水平面内,磁场方向竖直向下,金属棒ab与导轨接触良好,为使大圆环中产生图示电流,则ab应当( )
 如图所示,两同心金属圆环共面,其中大闭合圆环与导轨绝缘,小圆环的开口端点与导轨相连,平行导轨处在水平面内,磁场方向竖直向下,金属棒ab与导轨接触良好,为使大圆环中产生图示电流,则ab应当( )
如图所示,两同心金属圆环共面,其中大闭合圆环与导轨绝缘,小圆环的开口端点与导轨相连,平行导轨处在水平面内,磁场方向竖直向下,金属棒ab与导轨接触良好,为使大圆环中产生图示电流,则ab应当( )| A. | 向右加速运动 | B. | 向右减速运动 | C. | 向左加速运动 | D. | 向左减速运动 |
10.如图甲所示,在杂技表演中,猴子沿竖直杆向上运动,其v-t图象如图乙所示,人顶杆沿水平地面运动的x-t图象如图丙所示.若以地面为参考系,下列说法正确的是( )
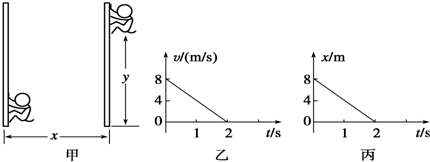

| A. | 猴子的运动轨迹为直线 | |
| B. | 猴子在2 s内做匀变速曲线运动 | |
| C. | t=0时猴子的速度大小为8 m/s | |
| D. | t=2 s时猴子的加速度大小为2 m/s2 |
8.一定质量的理想气体,状态变化过程如V-T图象中ABC图线所示,由图线可知( )
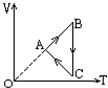

| A. | A→B过程,气体吸热、压强增大 | |
| B. | B→C过程,气体放热、压强增大 | |
| C. | C→A过程,分子密度减小 | |
| D. | C→A过程,分子在单位时间内撞击单位面积容器壁的次数增加 |
 如图所示,斜面AB、水平轨道BC和半圆形轨道CD平滑连接,AB、BC和CD处于同一平面内,CD的半径为R=0.4m.质量m=0.5kg的小球(可看做质点)从A点静止开始下滑,恰能到达D点.不计一切摩擦,g取10m/s2,求:
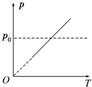
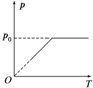
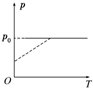
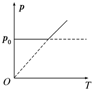
如图所示,斜面AB、水平轨道BC和半圆形轨道CD平滑连接,AB、BC和CD处于同一平面内,CD的半径为R=0.4m.质量m=0.5kg的小球(可看做质点)从A点静止开始下滑,恰能到达D点.不计一切摩擦,g取10m/s2,求: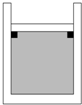 如图所示,U形气缸固定在水平地面上,用重力不计的活塞封闭着一定质量的气体,已知气缸不漏气,活塞移动过程无摩擦.初始时,外界大气压强为p0,活塞紧压小挡板.现缓慢升高缸内气体的温度,则图中能反映气缸内气体的压强p随热力学温度T变化的图象是( )
如图所示,U形气缸固定在水平地面上,用重力不计的活塞封闭着一定质量的气体,已知气缸不漏气,活塞移动过程无摩擦.初始时,外界大气压强为p0,活塞紧压小挡板.现缓慢升高缸内气体的温度,则图中能反映气缸内气体的压强p随热力学温度T变化的图象是( )