题目内容
19.如图甲所示,一对平行金属板M?N长为L,相距为d,O1O为中轴线.当两板间加电压UMN=U0时,两板间为匀强电场,忽略两极板外的电场?某种带负电的粒子从O1点以速度v0沿O1O方向射入电场,粒子恰好打在上极板M的中点,粒子重力忽略不计?
(1)求带电粒子的比荷$\frac{q}{m}$
(2)若MN间加如图乙所示的交变电压,其周期T=$\frac{T}{{v}_{0}}$,从t=0开始,前$\frac{T}{3}$内UMN=2U,后$\frac{2T}{3}$内UMN=-U,大量的上述粒子仍然以速度v0沿O1O方向持续射入电场,最终所有粒子恰好能全部离开电场而不打在极板上,求U的值;
(3)若紧贴板右侧建立xOy坐标系,在坐标系第I?IV象限某区域内存在一个方向垂直于坐标平面的圆形匀强磁场区域,能使在(2)问情景下所有粒子经过磁场偏转后都会聚于P(2d,2d)点,求此圆形磁场的最小面积及对应磁感应强度B的大小?
分析 (1)粒子在电场中做类平抛运动,由运动的合成与分解规律可求得比荷;
(2)由题意可知粒子在电场中的运动过程,根据电场的周期性变化规律可明确粒子在电场中的运动规律,根据条件则可求得电压值;
(3)所有粒子在磁场中均做匀速圆周运动,根据题意由几何关系求出磁场区的最小半径,从而得出最小面积.根据半径公式求出磁感应强度的大小.
解答 解:(1)设粒子经过时间t0打在M板中点,
沿极板方向有$\frac{L}{2}={v}_{0}{t}_{0}$,
垂直极板方向有$\frac{d}{2}=\frac{q{U}_{0}}{2md}{{t}_{0}}^{2}$,
可解得$\frac{q}{m}=\frac{4{d}^{2}{{v}_{0}}^{2}}{{U}_{0}{L}^{2}}$,
(2)粒子通过两板时间$t=\frac{L}{{v}_{0}}=T$,
从t=0时刻开始,粒子在两板间运动时每个电压变化周期的前三分之一时间内方向垂直极板的加速度大小${a}_{1}=\frac{2qU}{md}$,
(或在每个电压变化周期的后三分之二时间内方向垂直极板的加速度大小${a}_{2}=\frac{qU}{md}$)
不同时刻从O1点进入电场的粒子在电场方向的速度vy随时间t变化的关系如答图所示.所有粒子刚好能全部离开电场而不打在极板上,可以确定在t=nT或$t=nT+\frac{1}{3}T$ 时刻进入电场的粒子恰好分别从极板右侧上下边缘处飞出.它们在电场方向偏转的距离最大.
$\frac{d}{2}=\frac{1}{2}({a}_{1}\frac{T}{3})T$,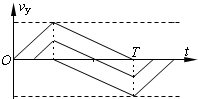
可解得$U=\frac{3{U}_{0}}{8}$.
(3)所有粒子射出电场时速度方向都平行于x轴,大小为v0.设粒子在磁场中的运动半径为r,则$q{v}_{0}B=m\frac{{{v}_{0}}^{2}}{r}$
可解得r=$\frac{m{v}_{0}}{qB}$.
粒子进入圆形区域内聚焦于P点时,磁场区半径R应满足R=r,
在圆形磁场区域边界上,P点纵坐标有最大值,如图所示.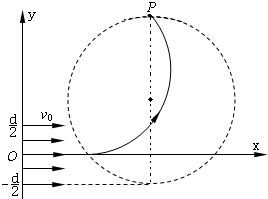
磁场区的最小半径$R=\frac{5}{4}d$,
圆形磁场的面积为$S=π{R}^{2}=\frac{25}{16}π{d}^{2}$.
磁感应强度B=$\frac{{U}_{0}{L}^{2}}{5{d}^{3}{v}_{0}}$.
答:(1)带电粒子的比荷为$\frac{4{d}^{2}{{v}_{0}}^{2}}{{U}_{0}{L}^{2}}$;
(2)U的值为$\frac{3{U}_{0}}{8}$;
(3)圆形磁场的最小面积为$\frac{25}{16}π{d}^{2}$,磁感应强度B的大小为$\frac{{U}_{0}{L}^{2}}{5{d}^{3}{v}_{0}}$.
点评 本题考查带电粒子在磁场中的运动,要注意电场中类平抛运动运动由运动的合成与分解求解;而磁场中的圆周运动解题的关键在于几何关系的把握.

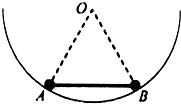 如图所示,质量均为m的两个小球A、B固定在轻杆的两端,将其放入光滑的半圆形碗中,杆的长度等于碗的半径,当杆与碗的竖直半径垂直时,两小球刚好能平衡,则小球A对碗的压力大小为( )
如图所示,质量均为m的两个小球A、B固定在轻杆的两端,将其放入光滑的半圆形碗中,杆的长度等于碗的半径,当杆与碗的竖直半径垂直时,两小球刚好能平衡,则小球A对碗的压力大小为( )| A. | $\frac{{\sqrt{3}}}{2}$mg | B. | $\frac{{2\sqrt{3}}}{3}$mg | C. | $\frac{{\sqrt{3}}}{3}$mg | D. | 2mg |
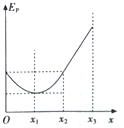 一带正电的粒子只在电场力作用下沿x轴正向运动,其电势能EP随位置x变化的关系如图所示,其中0~x2段是关于直线x=x1对称的曲线,x2~x3段是直线,且x3-x2=x2-x1,则下列说法正确的是( )
一带正电的粒子只在电场力作用下沿x轴正向运动,其电势能EP随位置x变化的关系如图所示,其中0~x2段是关于直线x=x1对称的曲线,x2~x3段是直线,且x3-x2=x2-x1,则下列说法正确的是( )| A. | 0~x1段的电场强度逐渐增大 | |
| B. | x1、x2、x3处电势φ1、φ2、φ3的关系为φ1<φ2<φ3 | |
| C. | 粒子在x1-x2段做匀变速运动,x2-x3段做匀速运动 | |
| D. | x1、x2两点间的电势差x2、x3两点间的大 |
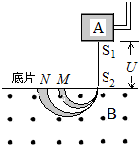 质谱仪最初是由汤姆生的学生阿斯顿设计的,他用质谱仪证实了同位素的存在.如图所示,容器A中有质量分别为m1,m2,电荷量相同的两种粒子(不考虑粒子重力及粒子间的相互作用),它们从容器A下方的小孔S1不断飘入电压为U的加速电场(粒子的初速度可视为零),沿直线S1S2(S2为小孔)与磁场垂直的方向进入磁感应强度为B、方向垂直纸面向外的匀强磁场中,最后打在水平放置的照相底片上.由于实际加速电压的天小在U士△U范围内微小变化,这两种粒子在底片上可能发生重叠.对此,下列判断正确的有( )
质谱仪最初是由汤姆生的学生阿斯顿设计的,他用质谱仪证实了同位素的存在.如图所示,容器A中有质量分别为m1,m2,电荷量相同的两种粒子(不考虑粒子重力及粒子间的相互作用),它们从容器A下方的小孔S1不断飘入电压为U的加速电场(粒子的初速度可视为零),沿直线S1S2(S2为小孔)与磁场垂直的方向进入磁感应强度为B、方向垂直纸面向外的匀强磁场中,最后打在水平放置的照相底片上.由于实际加速电压的天小在U士△U范围内微小变化,这两种粒子在底片上可能发生重叠.对此,下列判断正确的有( )| A. | 两粒子均带正电 | B. | 打在M处的粒子质量较小 | ||
| C. | 若U一定,△U越大越容易发生重叠 | D. | 若△U一定,U越大越容易发生重叠 |
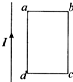
| A. | 若线圈向右平动,其中感应电流方向是abcda | |
| B. | 若线圈在线圈平面内沿电流方向平动,无感应电流产生 | |
| C. | 当线圈以ab边为轴转动时,其中感应电流方向是abcda | |
| D. | 当线圈向导线靠近时,其中感应电流方向是abcda |
| A. | 重力势能一定增加,动能一定减少 | |
| B. | 重力势能一定减少,动能一定增加 | |
| C. | 重力势能一定减少,动能不一定增加 | |
| D. | 重力势能不一定减少,动能不一定增加 |
 如图所示蹦蹦球是一种儿童健身玩具,某同学在17℃的室内对蹦蹦球充气,已知充气前球的总体积为2L,压强为latm,充气筒每次充入0.2L压强为latm的气体,忽略蹦蹦球体积变化及充气过程中气体温度的变化,求:
如图所示蹦蹦球是一种儿童健身玩具,某同学在17℃的室内对蹦蹦球充气,已知充气前球的总体积为2L,压强为latm,充气筒每次充入0.2L压强为latm的气体,忽略蹦蹦球体积变化及充气过程中气体温度的变化,求:
 如图所示,斜面AB、水平轨道BC和半圆形轨道CD平滑连接,AB、BC和CD处于同一平面内,CD的半径为R=0.4m.质量m=0.5kg的小球(可看做质点)从A点静止开始下滑,恰能到达D点.不计一切摩擦,g取10m/s2,求:
如图所示,斜面AB、水平轨道BC和半圆形轨道CD平滑连接,AB、BC和CD处于同一平面内,CD的半径为R=0.4m.质量m=0.5kg的小球(可看做质点)从A点静止开始下滑,恰能到达D点.不计一切摩擦,g取10m/s2,求: