��Ŀ����
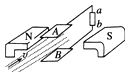
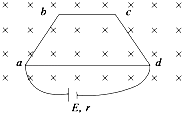
����Ŀ����ͼ��ʾ���㹻���Ĺ⻬ƽ�н�������cd��ef��ˮƽ���������L��������˸��̶�һ���뾶Ϊr���ķ�֮�������⻬Բ������Բ����ƽ������ֱ����ˮƽ�����Բ���ϸ���һ���뵼�촹ֱ�Ľ����ˣ�����������ˮƽ���졢����Բ���γɱպϻ�·����������������Ϊm�������ΪR��������費�ƣ�����װ�÷��ڴŸ�Ӧǿ�ȴ�СΪB��������ֱ���ϵ���ǿ�ų��У�����ˮƽ���ҵĺ���F= ![]() mg��ϸ��a���ﵽ�����˶�ʱ����bǡ�þ�ֹ��Բ����ij��������
mg��ϸ��a���ﵽ�����˶�ʱ����bǡ�þ�ֹ��Բ����ij��������
��1����a�������˶�ʱ����·�еĸ�Ӧ������
��2����a�������˶�ʱ���ٶȣ�
��3����b��ֹ��λ�þ�Բ����͵�ĸ߶ȣ�
���𰸡�
��1��
�⣺a�������˶�ʱ�������밲����ƽ�⣬F=BIL
�ã�I= ![]()
��2��
�⣺������a�и�Ÿ��ߣ������ĵ綯��E=BLv
��·����I= ![]() �����ã�v=
�����ã�v= ![]()
��3��
�⣺b��ƽ��ʱ�������Բ�ĵ���������ֱ����ļн�Ϊ�ȣ�
����tan ![]() =
= ![]() ���=60��
���=60��
����h=r��1��cos�ȣ�= ![]()
����������1����a�������˶�ʱ������F�밲����ƽ�⣬�ɰ�������ʽ����Ӧ��������2�����ݱպϵ�·ŷķ���������Ӧ�綯�ƣ��ɸ�Ӧ�綯�ƹ�ʽ�����a�������˶�ʱ���ٶȣ���3����bΪ�о�����b�ܵ��İ�������С��a�ܵ��İ�������С��ȣ�����ƽ�����������b��ֹ��λ�þ�Բ����͵�ĸ߶�

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д�