题目内容
【题目】“嫦娥二号”探月卫星沿地月转移轨道到达月球附近,在P点进行第一次“刹车制动”后被月球捕获,进入椭圆轨道绕月飞行,如图所示.已知“嫦娥二号”的质量为m,远月点Q距月球表面的高度为h,运行到Q点时它的角速度为ω,加速度为a,月球的质量为M、半径为R,月球表面的重力加速度为g,万有引力常量为G.则它在远月点时对月球的万有引力大小为( )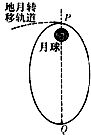
A.![]()
B.ma
C.![]()
D.m(R+h)ω2
【答案】B,C
【解析】解:设卫星在月球表面对月球的万有引力即重力为F1,在远月点时对月球的万有引力为F;
A、据万有引力公式得在远月点时对月球的万有引力为 ![]() ,故A错误;
,故A错误;
B、据力与运动的关系得在远月点时卫星所受合力即万有引力 F=ma;故B正确;
C、据万有引力公式得在月球表面时卫星所受重力即二者万有引力 ![]() ①
①
在远月点时卫星对月球的万有引力 ![]() =
= ![]() ②
②
把①代入②可得 ![]() 故C正确;
故C正确;
D、此公式适用于匀速圆周运动,而卫星在绕月椭圆运动时速度变化不均匀,不适用.
此题选择正确项,故选 BC.
根据题目信息可知,此题主要考查卫星公转地的椭圆轨道远月点万有引力即向心力问题.A、使用万有引力定律完全可以解决;B、结合力与运动的关系可解决;C、比较月球表面和远月点的万有引力可解决;D、此公式适用于匀速圆周运动.

练习册系列答案
相关题目