题目内容
9.法拉第在研究电磁感应现象的过程中发现:“电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比”.这就是著名的法拉第电磁感应定律,请根据定律完成下列问题.
(1)如图1所示,固定于水平面上的金属框架abcd,处在竖直向下的匀强磁场中.金属棒MN沿框架以速度v向右做匀速运动.框架的ab与dc平行,bc与ab、dc垂直.MN与bc的长度均为l,在运动过程中MN始终与bc平行,且与框架保持良好接触.磁场的磁感应强度为B.请根据法拉第电磁感应定律,证明金属棒MN中的感应电动势E=Blv;
(2)为进一步研究导体做切割磁感线运动的过程,现构建如下情景:
金属棒a和b,两棒质量都为m,电阻分别为Ra和Rb如图2所示,a棒从h高处自静止沿弧形轨道下滑,两导轨间距为L,通过C点进入轨道的水平部分,该水平部分存在竖直向下的匀强磁场,磁感应强度大小为B.(下滑时棒始终保持与导轨垂直)
a.若金属棒b固定于轨道的水平部分,且a棒始终没有跟b棒相碰,求a棒上最终产生的焦耳热(不计一切摩擦).
b.若金属棒b解除固定,静止于轨道水平部分,要使ab不相碰,b棒至少距离C点多远.
分析 (1)在△t时间内,ab棒向右移动的距离为,求出线框的磁通量的变化量,然后代入法拉第电磁感应定律即可得出E=BLv的结论;
(2)①根据能量守恒定律,回路中产生的焦耳热总量为mgh.ab棒串联,功率与电阻成正比
②由动能定理知C点速度,由动量守恒知ab的共同速度,由动量定理列式求解b棒至少距离C点多远.
解答 解:(1)在△t时间内,ab棒向右移动的距离为△x=v△t,这个过程中线框的面积变化量是:
△S=Lv△t
穿过闭合回路的磁通量的变化量是:△Φ=B△S=B Lv△t
根据法拉第电磁感应定律:E=n$\frac{△∅}{△t}$=1×$\frac{BLv△t}{△t}$=BLv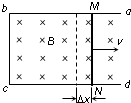
(2)
a、根据能量守恒定律,回路中产生的焦耳热总量为mgh.
ab棒串联,功率与电阻成正比,所以a棒上产生的热量为Q=$\frac{{R}_{a}mgh}{{R}_{a}+{R}_{b}}$
b、a棒滑至C点时的速度为vc=$\sqrt{2gh}$,a棒进入水平后和b棒组成的系统动量守恒定律.
由mvv=2mv2,得最终ab的速度均为v2=$\frac{1}{2}\sqrt{2gh}$
设ab棒的刚好达到相同速度的过程中的某时刻,ab的速度差为△v,则此时回路中产生的感应电动势Ei=$\frac{△∅}{△t}$=$\frac{BL△x}{△t}$=BL△v
此时回路中的感应电流Ii=$\frac{BL△v}{{R}_{a}+{R}_{b}}$
此时ab棒所受安培力Fi=BIiL=$\frac{{B}^{2}{L}^{2}△v}{{R}_{a}+{R}_{b}}$
对b棒根据动量定理有:Fi△t=m△v2
对a、b棒刚好达到相同速度的过程求和
则有:$\sum_{i}^{n}$=$\frac{{B}^{2}{L}^{2}△v}{{R}_{a}+{R}_{b}}$△t=mv2,
即$\frac{{B}^{2}{L}^{2}△x}{{R}_{a}+{R}_{b}}$=mv2
又因v2=$\frac{1}{2}$$\sqrt{2gh}$
所以解得最小距离为△x=$\frac{m({R}_{a}+{R}_{b})}{2{B}^{2}{L}^{2}}$$\sqrt{2gh}$
答:(1)证明过程见解析;
(2)a.若金属棒b固定于轨道的水平部分,且a棒始终没有跟b棒相碰,a棒上最终产生的焦耳热Q为$\frac{{R}_{a}mgh}{{R}_{a}+{R}_{b}}$;
b.若金属棒b解除固定,静止于轨道水平部分,要使ab不相碰,b棒至少距离C点$\frac{m({R}_{a}+{R}_{b})}{2{B}^{2}{L}^{2}}$$\sqrt{2gh}$.
点评 本题的关键是会推导安培力的表达式,根据平衡条件、牛顿第二定律和能量守恒、动量定理、动量守恒定律研究电磁感应现象,难度比较大.

 如图,工厂利用皮带传输机把质量为m的货物从地面运送到高处的平台C上.皮带以一定的速度v顺时针转动.将货物无初速度地放在A处,货物在皮带上相对滑动时留下一段划痕,然后货物达到速度v随皮带到达平台.已知货物与皮带间的动摩擦因数为μ,皮带的倾角为θ,重力加速度为g.下列说法正确的是( )
如图,工厂利用皮带传输机把质量为m的货物从地面运送到高处的平台C上.皮带以一定的速度v顺时针转动.将货物无初速度地放在A处,货物在皮带上相对滑动时留下一段划痕,然后货物达到速度v随皮带到达平台.已知货物与皮带间的动摩擦因数为μ,皮带的倾角为θ,重力加速度为g.下列说法正确的是( )| A. | 货物从A到C的过程中,平均速度为$\frac{v}{2}$ | |
| B. | 若改变传送带的速率v,使其变小,皮带上留下的划痕长度变短 | |
| C. | 货物从A点运动到C点,传送带一直对货物做正功 | |
| D. | 货物达到速度v以后的运动过程中,传送带对货物的摩擦力做功的功率为μmgvcosθ |
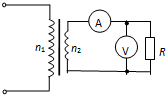 如图所示,一理想变压器原、副线圈匝数比n1:n2=11:5.原线圈与电压u=220$\sqrt{2}$sin(100πt)V正弦交变电源连接.副线圈仅接入一个100Ω的电阻.则( )
如图所示,一理想变压器原、副线圈匝数比n1:n2=11:5.原线圈与电压u=220$\sqrt{2}$sin(100πt)V正弦交变电源连接.副线圈仅接入一个100Ω的电阻.则( )| A. | 变压器副线圈的电压是220V | B. | 变压器的输入功率是100W | ||
| C. | 流过原线圈的电流的有效值为2.2A | D. | 电流表的示数为0.45A |
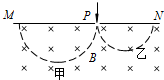 甲、乙两个带电粒子,以相同的速率经小孔P垂直磁场边界MN进入方向垂直纸面向里的匀强磁场中,在磁场中做匀速圆周运动,并垂直磁场边界MN射出磁场,半圆轨迹如图中虚线所示.不计粒子所受重力及空气阻力,则下列说法中正确的是( )
甲、乙两个带电粒子,以相同的速率经小孔P垂直磁场边界MN进入方向垂直纸面向里的匀强磁场中,在磁场中做匀速圆周运动,并垂直磁场边界MN射出磁场,半圆轨迹如图中虚线所示.不计粒子所受重力及空气阻力,则下列说法中正确的是( )| A. | 甲带正电,乙带负电 | |
| B. | 甲的荷质比小于乙的荷质比 | |
| C. | 甲、乙两个带电粒子从进入磁场到穿出磁场的过程中,洛伦兹力对甲、乙的冲量为零 | |
| D. | 甲的运行时间小于乙的运行的时间 |
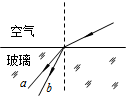 a、b两种单色光以相同的入射角从空气斜射向某种玻璃中,光路如图所示.关于a、b两种单色光,下列说法中正确的是( )
a、b两种单色光以相同的入射角从空气斜射向某种玻璃中,光路如图所示.关于a、b两种单色光,下列说法中正确的是( )| A. | 该种玻璃对b光的折射率较大 | |
| B. | b光在该玻璃中传播时的速度较大 | |
| C. | 两种单色光从该玻璃中射入空气发生全反射时,a光的临界角较小 | |
| D. | 在同样的条件下,分别用这两种单色光做双缝干涉实验,b光的干涉图样的相邻条纹间距较大 |
 、
、 均为理想电表,R、L和D分别是光敏电阻(其阻值随光强增大而减小)、理想线圈和灯泡.原线圈接入图乙所示的正弦交流电压u,下列说法中正确的是( )
均为理想电表,R、L和D分别是光敏电阻(其阻值随光强增大而减小)、理想线圈和灯泡.原线圈接入图乙所示的正弦交流电压u,下列说法中正确的是( )
| A. | 交流电的方向每秒钟改变50次 | |
| B. | 有光照射R时,D变亮 | |
| C. | 抽出L中的铁芯, 的示数变小 的示数变小 | |
| D. | 在t=0.005s时,电压表 的示数为22$\sqrt{2}$V 的示数为22$\sqrt{2}$V |
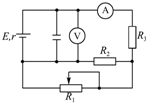 如图所示,电动势为E,内阻为r的电源与滑动变阻器R1、定值电阻R2、R3、平行板电容器及理想电表组成闭合电路.当滑动变阻器R1的触头向左移动一小段时,则( )
如图所示,电动势为E,内阻为r的电源与滑动变阻器R1、定值电阻R2、R3、平行板电容器及理想电表组成闭合电路.当滑动变阻器R1的触头向左移动一小段时,则( )| A. | 电流表读数增大 | B. | 电容器所带电荷量增加 | ||
| C. | R2消耗的功率减小 | D. | 电压表与电流表示数变化之比不变 |
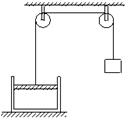 在图所示的气缸中封闭着温度为127℃的空气,一质量为m1的重物用绳索经滑轮与质量为m2的缸中活塞相连接,气缸截面积为S,大气压为P0重物和活塞均处于平衡状态,这时活塞离缸底的高度为10cm,不计一切摩擦.
在图所示的气缸中封闭着温度为127℃的空气,一质量为m1的重物用绳索经滑轮与质量为m2的缸中活塞相连接,气缸截面积为S,大气压为P0重物和活塞均处于平衡状态,这时活塞离缸底的高度为10cm,不计一切摩擦. 质量为m,电量为q的带正电小物块在磁感强度为B,方向垂直纸面向里的匀强磁场中,沿动摩擦因数为μ的绝缘水平面以初速度v0开始向左运动,如图所示.物块移动距离S1后停了下来,设此过程中,q不变.去掉磁场后,其他条件不变,物块移动距离S2后停了下来.则
质量为m,电量为q的带正电小物块在磁感强度为B,方向垂直纸面向里的匀强磁场中,沿动摩擦因数为μ的绝缘水平面以初速度v0开始向左运动,如图所示.物块移动距离S1后停了下来,设此过程中,q不变.去掉磁场后,其他条件不变,物块移动距离S2后停了下来.则