题目内容
16.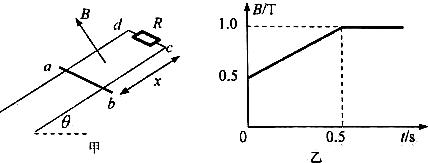 如图甲所示,宽L=0.5m、倾角θ=37°的两个相互平行的长金属导轨.上端c、d间接有R=0.5Ω的电阻.在导轨间存在垂直于导轨平面向上的磁场.磁感应强度B按图乙所示规律变化.一质量m=0.1kg的金属杆ab垂直轨道放置.距离上端电阻x=1.2m、t=0时ab由静止释放.最终以v=0.6m/s速度沿粗糙轨道向下匀速运动.除R外其余电阻均不计.滑动摩擦力等于最大静摩擦力.sin37°=0.6,cos37°=0.8,取g=10m/s2.
如图甲所示,宽L=0.5m、倾角θ=37°的两个相互平行的长金属导轨.上端c、d间接有R=0.5Ω的电阻.在导轨间存在垂直于导轨平面向上的磁场.磁感应强度B按图乙所示规律变化.一质量m=0.1kg的金属杆ab垂直轨道放置.距离上端电阻x=1.2m、t=0时ab由静止释放.最终以v=0.6m/s速度沿粗糙轨道向下匀速运动.除R外其余电阻均不计.滑动摩擦力等于最大静摩擦力.sin37°=0.6,cos37°=0.8,取g=10m/s2.(1)求ab匀速运动时R中的电流大小及方向;
(2)t>0.5s的某个时刻ab下滑速度为0.1m/s.求此时加速度的大小;
(3)通过推理说明ab何时开始运动.
分析 (1)根据法拉第电磁感应定律求感应电动势,由欧姆定律求电阻R中的电流,根据右手定则判断R中的电流方向;
(2)导体棒最终以v=0.6m/s的速度匀速运动,根据受力平衡求出摩擦力,t>0.5s的某个时刻ab下滑速度为0.1m/s,由牛顿第二定律求出加速度;
(3)0~0.5s内,回路产生感生电动势和感应电流,当ab达到最大静摩擦力时,ab开始滑动,求出磁感应强度,结合图象,求出开始运动的时刻
解答 解:(1)ab向下匀速运动时,根据右手定则,感应电流顺时针方向,流过R的电流方向d→c
最终匀速运动时感应电动势为:E=BLv=1×0.5×0.6=0.3V
R中的电流大小为:$I=\frac{E}{R}=\frac{0.3}{0.5}A=0.6A$
(2)最终以v=0.6m/s的速度匀速运动,根据受力平衡有:
$mgsin37°=\frac{{B}_{\;}^{2}{L}_{\;}^{2}v}{R}+f$…①
代入解得:f=0.3N
t>0.5s的某个时刻ab下滑速度为0.1m/s,根据牛顿第二定律,有:
$mgsin37°-\frac{{B}_{\;}^{2}{L}_{\;}^{2}v′}{R}-f=ma$…②
代入解得:$a=2.5m/{s}_{\;}^{2}$
(3)0~0.5s,感应电动势为:$E=\frac{△B}{△t}Lx=\frac{1-0.5}{0.5}×0.5×1.2=0.6V$
感应电流为:$I=\frac{E}{R}=\frac{0.6}{0.5}=1.2A$
mgsin37°=BIL+f
代入解得:B=0.5T,由图象知t=0时刻ab开始运动
答:(1)ab匀速运动时R中的电流大小0.6A及方向d→c;
(2)t>0.5s的某个时刻ab下滑速度为0.1m/s.此时加速度的大小$2.5m/{s}_{\;}^{2}$;
(3)t=0时ab开始运动
点评 解答本题的关键要能判断出棒ab的运动情况,再运用电路知识、电磁感应和力学知识,分析求解

 某同学在竖直悬挂的弹簧下加挂钩码,做实验研究弹力与弹簧伸长量的关系.下表是该同学的实验数据.实验时弹力始终未超过弹性限度,弹簧很轻,自身质量可以不计.g取10m/s2
某同学在竖直悬挂的弹簧下加挂钩码,做实验研究弹力与弹簧伸长量的关系.下表是该同学的实验数据.实验时弹力始终未超过弹性限度,弹簧很轻,自身质量可以不计.g取10m/s2(1)根据实验数据完成表格空白处的数据;并在坐标系中作出弹力F跟弹簧伸长量x关系图象.
(2)根据图象计算弹簧的劲度系数.
| 砝码质量m/g | 0 | 30 | 60 | 90 | 120 | 150 |
| 弹簧总长度L/cm | 6.0 | 7.2 | 8.3 | 9.5 | 10.6 | 11.8 |
| 弹力F/N | ||||||
| 弹簧伸长x/m |
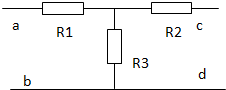 一个T型电路如图,电路中的电阻R1=10Ω,R2=120Ω,R3=40Ω,另有一测试电源,电动势为100V,内阻忽略不计,则( )
一个T型电路如图,电路中的电阻R1=10Ω,R2=120Ω,R3=40Ω,另有一测试电源,电动势为100V,内阻忽略不计,则( )| A. | 当cd端短路时,ab之间的等效电阻是130Ω | |
| B. | 当ab端短路时,cd之间的等效电阻是130Ω | |
| C. | 当ab端接通测试电源时,cd之间的电压为80V | |
| D. | 当cd端接通测试电源时,ab之间的电压为80V |
| A. | 跟穿过这一闭合电路的磁通量成正比 | |
| B. | 跟穿过这一闭合电路的磁通量的变化量成正比 | |
| C. | 跟穿过这一闭合电路的磁通量的变化率成正比 | |
| D. | 跟穿过这一闭合电路的磁感应强度成正比 |
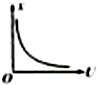
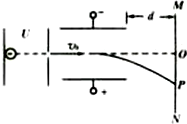 如图所示,一个电子由静止经过加速电压U的加速后,水平进入一平行板偏转电场,进入电场时电子速度与极板平行,最后打至荧光屏上的P点,若无偏转电场时电子打至O点.设OP=x,则x与U的x一U图象为( )
如图所示,一个电子由静止经过加速电压U的加速后,水平进入一平行板偏转电场,进入电场时电子速度与极板平行,最后打至荧光屏上的P点,若无偏转电场时电子打至O点.设OP=x,则x与U的x一U图象为( )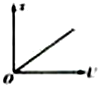
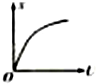
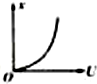
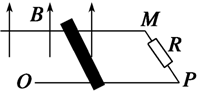 某学习小组在研究电磁感应实验中做了很多的探究.模型简化如下:如图,匀强磁场竖直向上穿过水平放置的金属框架,框架宽为L,右端接有电阻R,磁感应强度为B,一根质量为m、电阻为r的金属棒以v0的初速度沿框架向左运动,棒与框架的动摩擦因数为μ,测得棒运动的距离为S,则金属棒在速度为v0时两端的电压U=$\frac{R}{R+r}BL{v_0}$;整个过程中,流过电阻R的电量q=$\frac{BLS}{R+r}$,电阻R上的焦耳热Q$\frac{R}{R+r}({\frac{1}{2}mv_0^2-μmgS})$.
某学习小组在研究电磁感应实验中做了很多的探究.模型简化如下:如图,匀强磁场竖直向上穿过水平放置的金属框架,框架宽为L,右端接有电阻R,磁感应强度为B,一根质量为m、电阻为r的金属棒以v0的初速度沿框架向左运动,棒与框架的动摩擦因数为μ,测得棒运动的距离为S,则金属棒在速度为v0时两端的电压U=$\frac{R}{R+r}BL{v_0}$;整个过程中,流过电阻R的电量q=$\frac{BLS}{R+r}$,电阻R上的焦耳热Q$\frac{R}{R+r}({\frac{1}{2}mv_0^2-μmgS})$.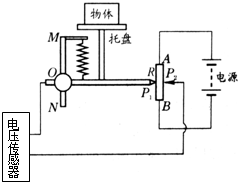 如图所示为某种测量物体质量的装置示意图,AB为一均匀的滑动变阻器,总阻值为R,长度为L,两边分别有P1、P2 两个滑动头,P1 可在竖直绝缘光滑的固定杆MN上保持水平状态而上下自由滑动.若P1、P2间出现电压时,可通过电压传感器测量出该电压U的大小.所用弹簧受到外力的大小与形变量的比值恒为已知值k,托盘自身质量不可忽略,电源电动势为E,内阻不计,当地的重力加速度为g.现用该装置测量待测物体的质量mx:
如图所示为某种测量物体质量的装置示意图,AB为一均匀的滑动变阻器,总阻值为R,长度为L,两边分别有P1、P2 两个滑动头,P1 可在竖直绝缘光滑的固定杆MN上保持水平状态而上下自由滑动.若P1、P2间出现电压时,可通过电压传感器测量出该电压U的大小.所用弹簧受到外力的大小与形变量的比值恒为已知值k,托盘自身质量不可忽略,电源电动势为E,内阻不计,当地的重力加速度为g.现用该装置测量待测物体的质量mx: