题目内容
8.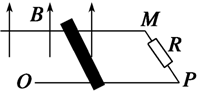 某学习小组在研究电磁感应实验中做了很多的探究.模型简化如下:如图,匀强磁场竖直向上穿过水平放置的金属框架,框架宽为L,右端接有电阻R,磁感应强度为B,一根质量为m、电阻为r的金属棒以v0的初速度沿框架向左运动,棒与框架的动摩擦因数为μ,测得棒运动的距离为S,则金属棒在速度为v0时两端的电压U=$\frac{R}{R+r}BL{v_0}$;整个过程中,流过电阻R的电量q=$\frac{BLS}{R+r}$,电阻R上的焦耳热Q$\frac{R}{R+r}({\frac{1}{2}mv_0^2-μmgS})$.
某学习小组在研究电磁感应实验中做了很多的探究.模型简化如下:如图,匀强磁场竖直向上穿过水平放置的金属框架,框架宽为L,右端接有电阻R,磁感应强度为B,一根质量为m、电阻为r的金属棒以v0的初速度沿框架向左运动,棒与框架的动摩擦因数为μ,测得棒运动的距离为S,则金属棒在速度为v0时两端的电压U=$\frac{R}{R+r}BL{v_0}$;整个过程中,流过电阻R的电量q=$\frac{BLS}{R+r}$,电阻R上的焦耳热Q$\frac{R}{R+r}({\frac{1}{2}mv_0^2-μmgS})$.
分析 由法拉第电磁感应定律可求得感应电动势E=BLv0,通过棒的电量由q=It可求;
由能的转化和守恒定律可求得R上产生的热量.
解答 解:当速度为v0时,产生的感应电动势E=BLv0,
根据并串联电压分布特点,得,U=$\frac{R}{R+r}BL{v_0}$;
由q=It=$\frac{BL{v}_{0}}{R+r}$•$\frac{S}{{v}_{0}}$=$\frac{BLS}{R+r}$;
根据能的转化和守恒定律,金属棒的动能的一部分克服摩擦力做功,一部分转化为电能,电能又转化为热能Q,
即$\frac{1}{2}$mv02=μmgs+Q,
Q=$\frac{1}{2}$mv02-μmgS,
根据并串联电热分布特点,得Q=$\frac{R}{R+r}({\frac{1}{2}mv_0^2-μmgS})$;
故答案为:$\frac{R}{R+r}BL{v_0}$;$\frac{BLS}{R+r}$;$\frac{R}{R+r}({\frac{1}{2}mv_0^2-μmgS})$.
点评 在考查导体切割磁感线的问题考查中,要注意正确应用能量守恒关系进行分析.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
3.把长度L、电流I都相同的一小段电流元放入某磁场中的A、B两点,电流元在A点受到的磁场力较大,则( )
| A. | A点的磁感应强度一定大于B点的磁感应强度 | |
| B. | A、B两点磁感应强度可能相等 | |
| C. | A、B两点磁感应强度一定不相等 | |
| D. | A点磁感应强度可能小于B点磁感应强度 |
13.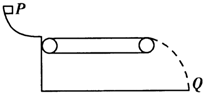 如图所示,物体从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带后落到地面上的Q点.若使传送带以某一速度匀速转动起来,再把物体放到P点自由滑下,则下列说法正确的是( )
如图所示,物体从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带后落到地面上的Q点.若使传送带以某一速度匀速转动起来,再把物体放到P点自由滑下,则下列说法正确的是( )
 如图所示,物体从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带后落到地面上的Q点.若使传送带以某一速度匀速转动起来,再把物体放到P点自由滑下,则下列说法正确的是( )
如图所示,物体从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带后落到地面上的Q点.若使传送带以某一速度匀速转动起来,再把物体放到P点自由滑下,则下列说法正确的是( )| A. | 若传送带逆时针方向转动时,物体将一定落在Q点的左边 | |
| B. | 若传送带逆时针方向转动时,物体将仍落在Q点 | |
| C. | 若传送带顺时针方向转动时,物体可能会落在Q点 | |
| D. | 若传送带顺时针方向转动时,物体将一定落在Q点的右边 |
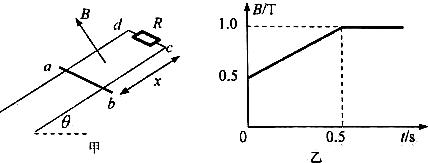 如图甲所示,宽L=0.5m、倾角θ=37°的两个相互平行的长金属导轨.上端c、d间接有R=0.5Ω的电阻.在导轨间存在垂直于导轨平面向上的磁场.磁感应强度B按图乙所示规律变化.一质量m=0.1kg的金属杆ab垂直轨道放置.距离上端电阻x=1.2m、t=0时ab由静止释放.最终以v=0.6m/s速度沿粗糙轨道向下匀速运动.除R外其余电阻均不计.滑动摩擦力等于最大静摩擦力.sin37°=0.6,cos37°=0.8,取g=10m/s2.
如图甲所示,宽L=0.5m、倾角θ=37°的两个相互平行的长金属导轨.上端c、d间接有R=0.5Ω的电阻.在导轨间存在垂直于导轨平面向上的磁场.磁感应强度B按图乙所示规律变化.一质量m=0.1kg的金属杆ab垂直轨道放置.距离上端电阻x=1.2m、t=0时ab由静止释放.最终以v=0.6m/s速度沿粗糙轨道向下匀速运动.除R外其余电阻均不计.滑动摩擦力等于最大静摩擦力.sin37°=0.6,cos37°=0.8,取g=10m/s2.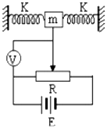 如图所示为一种加速度仪的示意图.质量为 m 的振子两端连有劲度系数均为 k 的轻弹簧,电源的电动势为 E,不计内阻,滑动变阻器的总阻值为 R,有效长度为 L,系统静止时,滑动触头位于滑动变阻器正中,这时电压表指针恰好在刻度盘正中.
如图所示为一种加速度仪的示意图.质量为 m 的振子两端连有劲度系数均为 k 的轻弹簧,电源的电动势为 E,不计内阻,滑动变阻器的总阻值为 R,有效长度为 L,系统静止时,滑动触头位于滑动变阻器正中,这时电压表指针恰好在刻度盘正中.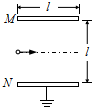 如图所示,平行金属板M、N的板长和板间距离都是l,N极板接地.电子束从静止开始,经电压U0加速后,沿M、N的中线连续不断地从左端射入两板间.电子电量为e,质量为m.不考虑重力和电子间的相互作用力.求:
如图所示,平行金属板M、N的板长和板间距离都是l,N极板接地.电子束从静止开始,经电压U0加速后,沿M、N的中线连续不断地从左端射入两板间.电子电量为e,质量为m.不考虑重力和电子间的相互作用力.求: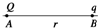 场源电荷Q=2×10-4 C,是正点电荷.检验电荷q=-2×10-5 C,是负点电荷,它们相距r=2m,且都在真空中,静电力常量k=9.0×109N•m2/C2,如图所示.求:
场源电荷Q=2×10-4 C,是正点电荷.检验电荷q=-2×10-5 C,是负点电荷,它们相距r=2m,且都在真空中,静电力常量k=9.0×109N•m2/C2,如图所示.求: