题目内容
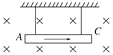
【题目】如图所示,BCDG是光滑绝缘的![]() 圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中,现有一质量为m带正电的小滑块(可视为质点)置于水平轨道上,滑块从水平轨道上距离B点S=3R的A点由静止释放,滑块到达与圆心
圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中,现有一质量为m带正电的小滑块(可视为质点)置于水平轨道上,滑块从水平轨道上距离B点S=3R的A点由静止释放,滑块到达与圆心![]() 等高的
等高的![]() 点时,
点时,![]() =
=![]() ,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.(
,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.(![]()
![]() ) 求 :
) 求 :

(1)小滑块受到电场力F=?
(2) 若改变s的大小,使滑块恰好始终沿轨道滑行,且从G点飞出,滑块在圆轨道上滑行过程中的最小动能为多少?
(3) 在(2)问中,滑块经过G点速度![]() =?
=? ![]()
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)A到C,由动能定理得:![]()
解得:F=0.75mg
(2)电场力与重力的合力 ![]()
当合力F′恰好提供向心力时,速度最小:
![]()
解得:![]()
(3)在动能最小处,合力方向与竖直方向夹角θ=370![]()
从动能最小的点到G点过程由动能定理得:![]()
解得:![]()

练习册系列答案
相关题目