题目内容
15. 如图所示,质量为mB=14kg的木板B放在水平地面上,质量为mA=10kg的货箱A放在木板B上.一根轻绳一端拴在货箱上,另一端拴在地面的木桩上,绳绷紧时与水平面的夹角为θ=37°.已知货箱A与木板B之间的动摩擦因数μ1=0.5,木板B与地面之间的动摩擦因数μ2=0.4.重力加速度g取10m/s2.现用水平力F将木板B从货箱A下面匀速抽出,试求:
如图所示,质量为mB=14kg的木板B放在水平地面上,质量为mA=10kg的货箱A放在木板B上.一根轻绳一端拴在货箱上,另一端拴在地面的木桩上,绳绷紧时与水平面的夹角为θ=37°.已知货箱A与木板B之间的动摩擦因数μ1=0.5,木板B与地面之间的动摩擦因数μ2=0.4.重力加速度g取10m/s2.现用水平力F将木板B从货箱A下面匀速抽出,试求:(1)绳上张力T的大小;
(2)拉力F的大小.(sin37°=0.6,cos37°=0.8)
分析 (1)对木块A受力分析,受到重力、支持力、B对A的摩擦力和细线的拉力,根据共点力平衡条件列式求解即可;
(2)对木块B受力分析,受到重力、A对B的压力和摩擦力、地面的支持力和摩擦力,最后根据共点力平衡条件列式求解即可.
解答  解:(1)对A物体进行受力分析,有四个力作用,分解绳的拉力,根据A物体平衡可得:
解:(1)对A物体进行受力分析,有四个力作用,分解绳的拉力,根据A物体平衡可得:
N1=mAg+Tsinθ
F1=Tcosθ F1=μ1N1
解得:T=$\frac{μ1mAg}{cosθ-μ1sinθ}$
代入数据得:T=100 N.
(2)对B进行受力分析,受六个力的作用,地面对B的支持力为:
N2=mBg+N1
地面对B的摩擦力为:F2=μN2
F=F1+F2=200 N.
答:(1)绳上张力T为100N;
(2)拉力F的为200N.
点评 本题关键是先后对木块A和木块B受力分析,然后根据共点力平衡条件并运用正交分解法列方程求解.

练习册系列答案
相关题目
3.关于力和运动的关系,下面说法正确的是( )
| A. | 静止的物体一定没有受到力的作用 | |
| B. | 运动的物体不受力就会停止下来 | |
| C. | 正在运动的物体一定受到力的作用 | |
| D. | 运动的物体,如果不受力的作用,将永远运动下去 |
10.物体自离地足够高做竖直上抛运动(不计阻力),在落回抛出点时该物体的速率是30m/s,那么物体(g取10m/s2)( )
| A. | 由抛出到落回抛出点的时间是6s | |
| B. | 只有在抛出后2s末时经过40m高处 | |
| C. | 经过距抛出点25m处时的瞬时速率只能是20 m/s | |
| D. | 离开抛出点后能上升的最大高度是45m |
7. 如图所示,三个同心圆是同一个点电荷周围的三个等势面,已知这三个圆的半径之差相等.A、B、C分别是这三个等势面上的点,且在同一条电场线上.A、C两点的电势依次为φA=8V和φC=6V,则B点的电势是( )
如图所示,三个同心圆是同一个点电荷周围的三个等势面,已知这三个圆的半径之差相等.A、B、C分别是这三个等势面上的点,且在同一条电场线上.A、C两点的电势依次为φA=8V和φC=6V,则B点的电势是( )
 如图所示,三个同心圆是同一个点电荷周围的三个等势面,已知这三个圆的半径之差相等.A、B、C分别是这三个等势面上的点,且在同一条电场线上.A、C两点的电势依次为φA=8V和φC=6V,则B点的电势是( )
如图所示,三个同心圆是同一个点电荷周围的三个等势面,已知这三个圆的半径之差相等.A、B、C分别是这三个等势面上的点,且在同一条电场线上.A、C两点的电势依次为φA=8V和φC=6V,则B点的电势是( )| A. | 一定等于7V | B. | 一定低于7V | C. | 一定高于7V | D. | 无法确定 |
4.通过打点计时器得到的一条纸带上的点迹不均匀,下列判断正确的是( )
| A. | 点迹密集的地方物体运动的速度较大 | |
| B. | 点迹密集的地方物体运动的速度较小 | |
| C. | 点迹不均匀说明物体做变速运动 | |
| D. | 点迹不均匀说明相邻两点之间的时间间隔不同 |
5.一物体做匀变速直线运动,速度图象如图所示,设向右为正方向,则前4s内( )


| A. | 物体始终向右运动 | |
| B. | 在t=2s时,物体距出发点最远 | |
| C. | 物体先向左运动,2s后开始向右运动 | |
| D. | 物体前2s位于出发点的左方,后2s位于出发点的右方 |
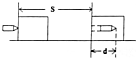 飞行子弹打入放在光滑水平面上的木块中深入2cm,未穿出同时木块滑动了1cm,则子弹动能的变化、木块获得的动能、由于摩擦增加的内能的比是多少?
飞行子弹打入放在光滑水平面上的木块中深入2cm,未穿出同时木块滑动了1cm,则子弹动能的变化、木块获得的动能、由于摩擦增加的内能的比是多少?