题目内容
9.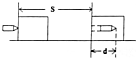 飞行子弹打入放在光滑水平面上的木块中深入2cm,未穿出同时木块滑动了1cm,则子弹动能的变化、木块获得的动能、由于摩擦增加的内能的比是多少?
飞行子弹打入放在光滑水平面上的木块中深入2cm,未穿出同时木块滑动了1cm,则子弹动能的变化、木块获得的动能、由于摩擦增加的内能的比是多少?
分析 子弹受到摩擦阻力,而木块所受到摩擦动力,两者摩擦力f大小相等,可认为是恒力.运用动能定理分别研究子弹和木块,求出各自的动能变化.
子弹与木块的总动能减少,转化为内能,根据Q=fd,d是相对位移大小求系统总机械能的损失.
解答 解:子弹对木块的作用力大小为f,木块相对于地的位移为L,则子弹对木块做功为fL,
根据动能定理得知,木块动能的增加量等于子弹对木块做的功,即为fL.
木块对子弹的阻力做功为-f(L+d),根据动能定理得知:子弹动能的减少量等于子弹克服阻力做功,大小为f(L+d).
所以子弹动能的变化量与木块获得的动能之比是(L+d):L=(1+2):1=3:1;
子弹相对于木块的位移大小为d,则系统克服阻力做功为fd,根据功能关系可知,系统增加的内能为:fd.
子弹减少的动能跟系统增加的内能之比为(L+d):d=(1+2):2=3:2;
答:子弹动能的变化、木块获得的动能之比为3:1;子弹动能变化与系统增加的内能之比为3:2.
点评 本题关键是掌握动能定理,并能用来处理子弹打木块的问题,要注意对子弹和木块而言,位移是相对于地的位移,不是子弹相对于木块的位移.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
19. 如图所示,两根细线挂着两个质量相同的小球A,B,原来两球不带电时,上、下两根细线的拉力为FA,FB,现在两球带上同种电荷后,上、下两根细线的拉力分别为FA′,FB′,则( )
如图所示,两根细线挂着两个质量相同的小球A,B,原来两球不带电时,上、下两根细线的拉力为FA,FB,现在两球带上同种电荷后,上、下两根细线的拉力分别为FA′,FB′,则( )
 如图所示,两根细线挂着两个质量相同的小球A,B,原来两球不带电时,上、下两根细线的拉力为FA,FB,现在两球带上同种电荷后,上、下两根细线的拉力分别为FA′,FB′,则( )
如图所示,两根细线挂着两个质量相同的小球A,B,原来两球不带电时,上、下两根细线的拉力为FA,FB,现在两球带上同种电荷后,上、下两根细线的拉力分别为FA′,FB′,则( )| A. | FA=FA′,FB>FB′ | B. | FA=FA′,FB<FB′ | C. | FA<FA′,FB>FB′ | D. | FA>FA′,FB>FB′ |


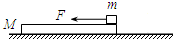 如图所示,质量为M=5kg的木板静止在光滑的水平面上,木板的上端有一质量为m=4kg的木块,以水平向左的恒力F=15N作用于木块上.已知木块与木板间的动摩擦因数μ=0.5,求4s内摩擦力对木板做的功.(最大静摩擦力等于滑动摩擦力).
如图所示,质量为M=5kg的木板静止在光滑的水平面上,木板的上端有一质量为m=4kg的木块,以水平向左的恒力F=15N作用于木块上.已知木块与木板间的动摩擦因数μ=0.5,求4s内摩擦力对木板做的功.(最大静摩擦力等于滑动摩擦力). 如图所示,质量为mB=14kg的木板B放在水平地面上,质量为mA=10kg的货箱A放在木板B上.一根轻绳一端拴在货箱上,另一端拴在地面的木桩上,绳绷紧时与水平面的夹角为θ=37°.已知货箱A与木板B之间的动摩擦因数μ1=0.5,木板B与地面之间的动摩擦因数μ2=0.4.重力加速度g取10m/s2.现用水平力F将木板B从货箱A下面匀速抽出,试求:
如图所示,质量为mB=14kg的木板B放在水平地面上,质量为mA=10kg的货箱A放在木板B上.一根轻绳一端拴在货箱上,另一端拴在地面的木桩上,绳绷紧时与水平面的夹角为θ=37°.已知货箱A与木板B之间的动摩擦因数μ1=0.5,木板B与地面之间的动摩擦因数μ2=0.4.重力加速度g取10m/s2.现用水平力F将木板B从货箱A下面匀速抽出,试求: