Question

【题目】如图所示，有一条长为L、质量为m的均匀金属链条，一半长度在光滑斜面上，斜面倾角为θ，另一半长度沿竖直方向下垂在空中，当链条从静止开始释放后链条滑动，以斜面最高点为重力势能的零点，求：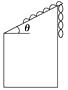

（1）开始时和链条刚好从右侧全部滑出斜面时重力势能各是多大？
（2）此过程中重力势能减少了多少？

Answer 1

【答案】
（1）解：开始时，左边一半链条重力势能为
Ep1＝－ g· sin θ，
右边一半的重力势能为Ep2＝－ g· ，
左右两部分总的重力势能为
Ep＝Ep1＋Ep2＝－ mgL（1＋sin θ），
最后链条从右侧刚好全部滑出时，重力势能
Ep′＝－ mgL．
（2）解：重力势能减少了ΔEp减＝Ep－Ep′＝ mgL（3－sin θ）
【解析】此题属于典型题型，需引起重视，物体处于参考平面下方时重力势能为负，计算重力势能的大小时高度为物体重心离地面的高度，初始时链条左右两端所具有的重力势能不同，分别计算左右两部分重心离参考平面的高度。