题目内容
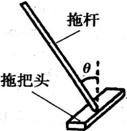 拖把是由拖杆和拖把头构成的擦地工具(如图).设拖把头的质量为m,拖杆质量可以忽略;拖把头与地板之间的动摩擦因数为常数μ,重力加速度为g,某同学用该拖把在水平地板上拖地时,沿拖杆方向推拖把,拖杆与竖直方向的夹角为θ.
拖把是由拖杆和拖把头构成的擦地工具(如图).设拖把头的质量为m,拖杆质量可以忽略;拖把头与地板之间的动摩擦因数为常数μ,重力加速度为g,某同学用该拖把在水平地板上拖地时,沿拖杆方向推拖把,拖杆与竖直方向的夹角为θ.
(1)若拖把头在地板上匀速移动,求推拖把的力的大小.
(2)设能使该拖把在地板上从静止刚好开始运动的水平推力与此时地板对拖把的正压力的比值为λ.已知存在一临界角θ0,若θ≤θ0,则不管沿拖杆方向的推力多大,都不可能使拖把从静止开始运动.求这一临界角的正切tanθ0.
解:(1)拖把头受到重力、支持力、推力和摩擦力处于平衡,设该同学沿拖杆方向用大小为F的力推拖把.
将推拖把的力沿竖直和水平方向分解,
按平衡条件有
竖直方向上:Fcosθ+mg=N ①
水平方向上:Fsinθ=f ②
式中N和f分别为地板对拖把的正压力和摩擦力.按摩擦定律有 f=μN ③
联立①②③式得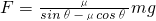 ④
④
(2)若不管沿拖杆方向用多大的力不能使拖把从静止开始运动,
应有Fsinθ≤λN ⑤
这时①式仍满足.联立①⑤式得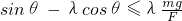 ⑥
⑥
现考察使上式成立的θ角的取值范围.
注意到上式右边总是大于零,且当F无限大时极限为零,
有sinθ-λcosθ≤0 ⑦
使上式成立的θ角满足θ≤θ0,这里θ0是题中所定义的临界角,
即当θ≤θ0时,不管沿拖杆方向用多大的力都推不动拖把.
临界角的正切为tanθ0=λ⑧
答:(1)若拖把头在地板上匀速移动,推拖把的力的大小为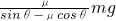 .
.
(2)tanθ0=λ.
分析:(1)对拖把头受力分析,抓住竖直方向和水平方向合力为零,运用正交分解求出推力F的大小.
(2)当推力F的水平分力小于等于最大静摩擦力时,不管沿拖杆方向的推力多大,都不可能使拖把从静止开始运动.结合第1问的结果,得到λ的表达式,采用极限法:当F无限大时的情况求解tanθ0.
点评:本题第1问是常规题,根据平衡条件,运用正交分解法求解推力.第2问是一种自锁现象,根据推不动的条件:推力的水平分力不大于最大静摩擦力出发进行分析求解.
将推拖把的力沿竖直和水平方向分解,
按平衡条件有
竖直方向上:Fcosθ+mg=N ①
水平方向上:Fsinθ=f ②
式中N和f分别为地板对拖把的正压力和摩擦力.按摩擦定律有 f=μN ③
联立①②③式得
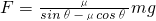 ④
④(2)若不管沿拖杆方向用多大的力不能使拖把从静止开始运动,
应有Fsinθ≤λN ⑤
这时①式仍满足.联立①⑤式得
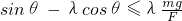 ⑥
⑥现考察使上式成立的θ角的取值范围.
注意到上式右边总是大于零,且当F无限大时极限为零,
有sinθ-λcosθ≤0 ⑦
使上式成立的θ角满足θ≤θ0,这里θ0是题中所定义的临界角,
即当θ≤θ0时,不管沿拖杆方向用多大的力都推不动拖把.
临界角的正切为tanθ0=λ⑧
答:(1)若拖把头在地板上匀速移动,推拖把的力的大小为
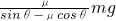 .
.(2)tanθ0=λ.
分析:(1)对拖把头受力分析,抓住竖直方向和水平方向合力为零,运用正交分解求出推力F的大小.
(2)当推力F的水平分力小于等于最大静摩擦力时,不管沿拖杆方向的推力多大,都不可能使拖把从静止开始运动.结合第1问的结果,得到λ的表达式,采用极限法:当F无限大时的情况求解tanθ0.
点评:本题第1问是常规题,根据平衡条件,运用正交分解法求解推力.第2问是一种自锁现象,根据推不动的条件:推力的水平分力不大于最大静摩擦力出发进行分析求解.

练习册系列答案
相关题目
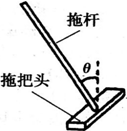 拖把是由拖杆和拖把头构成的擦地工具(如图).设拖把头的质量为m,拖杆质量可以忽略;拖把头与地板之间的动摩擦因数为常数μ,重力加速度为g,某同学用该拖把在水平地板上拖地时,沿拖杆方向推拖把,拖杆与竖直方向的夹角为θ.
拖把是由拖杆和拖把头构成的擦地工具(如图).设拖把头的质量为m,拖杆质量可以忽略;拖把头与地板之间的动摩擦因数为常数μ,重力加速度为g,某同学用该拖把在水平地板上拖地时,沿拖杆方向推拖把,拖杆与竖直方向的夹角为θ.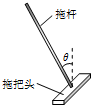 拖把是由拖杆和拖把头构成的擦地工具,如图所示.设拖把头的质量为m,拖杆质量可以忽略,拖杆与竖直方向的夹角为θ.某同学用该拖把在水平地板上拖地,当沿拖杆方向的推力为F时,拖把头在地板上匀速移动,则拖把头与地板之间的动摩擦因数μ为(重力加速度为g)( )
拖把是由拖杆和拖把头构成的擦地工具,如图所示.设拖把头的质量为m,拖杆质量可以忽略,拖杆与竖直方向的夹角为θ.某同学用该拖把在水平地板上拖地,当沿拖杆方向的推力为F时,拖把头在地板上匀速移动,则拖把头与地板之间的动摩擦因数μ为(重力加速度为g)( )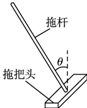 拖把是由拖杆和拖把头构成的擦地工具(如图).设拖把头的质量为0.5Kg,拖杆质量可忽略;拖把头与地板之间的动摩擦因数为0.5,重力加速度为10m/s2.某同学用该拖把在水平地板上拖地时,沿拖杆方向推拖把,拖杆与竖直方向的夹角为370,若拖把头在地板上匀速移动,求推拖把的力的大小(sin37°=0.6 cos37°=0.8)
拖把是由拖杆和拖把头构成的擦地工具(如图).设拖把头的质量为0.5Kg,拖杆质量可忽略;拖把头与地板之间的动摩擦因数为0.5,重力加速度为10m/s2.某同学用该拖把在水平地板上拖地时,沿拖杆方向推拖把,拖杆与竖直方向的夹角为370,若拖把头在地板上匀速移动,求推拖把的力的大小(sin37°=0.6 cos37°=0.8)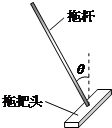 拖把是由拖杆和拖把头构成的擦地工具(如图).设拖把头的质量为m,拖杆质量可以忽略;拖把头与地板之间的动摩擦因数为μ,重力加速度为g,某同学用该拖把在水平地板上拖地时,沿拖杆方向推拖把,拖杆与竖直方向的夹角为θ.当拖把头在地板上匀速移动时推拖把的力F的大小为( )
拖把是由拖杆和拖把头构成的擦地工具(如图).设拖把头的质量为m,拖杆质量可以忽略;拖把头与地板之间的动摩擦因数为μ,重力加速度为g,某同学用该拖把在水平地板上拖地时,沿拖杆方向推拖把,拖杆与竖直方向的夹角为θ.当拖把头在地板上匀速移动时推拖把的力F的大小为( )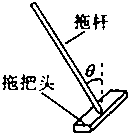 拖把是由拖杆和拖把头构成的擦地工具(如图).设拖把头的质量为m,拖杆质量可以忽略;拖把头与地板之间的动摩擦因数为常数μ,重力加速度为g,某同学用该拖把在水平地板上拖地时,沿拖杆方向推拖把,拖杆与竖直方向的夹角为θ.
拖把是由拖杆和拖把头构成的擦地工具(如图).设拖把头的质量为m,拖杆质量可以忽略;拖把头与地板之间的动摩擦因数为常数μ,重力加速度为g,某同学用该拖把在水平地板上拖地时,沿拖杆方向推拖把,拖杆与竖直方向的夹角为θ.