题目内容
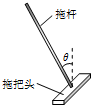拖把是由拖杆和拖把头构成的擦地工具，如图所示．设拖把头的质量为m，拖杆质量可以忽略，拖杆与竖直方向的夹角为θ．某同学用该拖把在水平地板上拖地，当沿拖杆方向的推力为F时，拖把头在地板上匀速移动，则拖把头与地板之间的动摩擦因数μ为（重力加速度为g）（ ）分析：对于拖把头受重力、支持力、推力和摩擦力，抓住水平方向和竖直方向平衡，根据正交分解，运用平衡条件和滑动摩擦力公式列方程，求出动摩擦因数μ．
解答：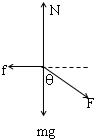
解：拖把头受到重力、支持力、推力和摩擦力处于平衡，受力示意图如图所示．
将推拖把的力沿竖直和水平方向分解，
按平衡条件得：
竖直方向上：Fcosθ+mg=N ①
水平方向上：Fsinθ=f ②
式中N和f分别为地板对拖把的正压力和摩擦力．按摩擦定律有 f=μN ③
联立解得，μ=
故选：B
解：拖把头受到重力、支持力、推力和摩擦力处于平衡，受力示意图如图所示．将推拖把的力沿竖直和水平方向分解，
按平衡条件得：
竖直方向上：Fcosθ+mg=N ①
水平方向上：Fsinθ=f ②
式中N和f分别为地板对拖把的正压力和摩擦力．按摩擦定律有 f=μN ③
联立解得，μ=
| Fsinθ |
| mg+Fcosθ |
故选：B
点评：解决本题的关键能够正确地进行受力分析，抓住合力为零，运用正交分解进行求解．
练习册系列答案
相关题目
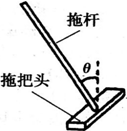拖把是由拖杆和拖把头构成的擦地工具（如图）．设拖把头的质量为m，拖杆质量可以忽略；拖把头与地板之间的动摩擦因数为常数μ，重力加速度为g，某同学用该拖把在水平地板上拖地时，沿拖杆方向推拖把，拖杆与竖直方向的夹角为θ．
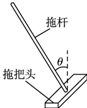拖把是由拖杆和拖把头构成的擦地工具（如图）．设拖把头的质量为0.5Kg，拖杆质量可忽略；拖把头与地板之间的动摩擦因数为0.5，重力加速度为10m/s2．某同学用该拖把在水平地板上拖地时，沿拖杆方向推拖把，拖杆与竖直方向的夹角为370，若拖把头在地板上匀速移动，求推拖把的力的大小（sin37°=0.6 cos37°=0.8）
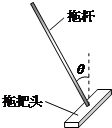拖把是由拖杆和拖把头构成的擦地工具（如图）．设拖把头的质量为m，拖杆质量可以忽略；拖把头与地板之间的动摩擦因数为μ，重力加速度为g，某同学用该拖把在水平地板上拖地时，沿拖杆方向推拖把，拖杆与竖直方向的夹角为θ．当拖把头在地板上匀速移动时推拖把的力F的大小为（ ）
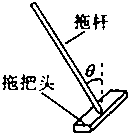拖把是由拖杆和拖把头构成的擦地工具（如图）．设拖把头的质量为m，拖杆质量可以忽略；拖把头与地板之间的动摩擦因数为常数μ，重力加速度为g，某同学用该拖把在水平地板上拖地时，沿拖杆方向推拖把，拖杆与竖直方向的夹角为θ．