题目内容
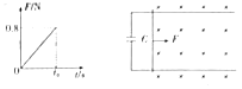
【题目】如图所示,两平行光滑导轨置于水平面(纸面)内,导轨间距L=0.5m,左端连有电容C=0.4F的电容器。一金属杆置于导轨上,金属杆右侧存在一磁感应强度B=1.0T,方向竖直向下的匀强磁场区域。金属杆在平行于导轨的拉力F作用下,沿导轨向右做初速度为零的加速直线运动,在金属杆的速度从零增大到v=2m/s的过程中,拉力F随时间t变化的图象如图所示。已知金属杆的质量m=0.1kg,电容器储存电能的表达式![]() (U为电容器两极板间的电压),金属杆与导轨始终保持垂直且接触良好,忽略一切电阻及电磁辐射的能量,求:
(U为电容器两极板间的电压),金属杆与导轨始终保持垂直且接触良好,忽略一切电阻及电磁辐射的能量,求:
(1)该过程拉力做的功W;
(2)该过程的时间t0
【答案】(1)该过程拉力做的功为0.4J;(2)该过程的时间为1s。
【解析】
(1)当速度为v时的感应电动势E=BLv
根据能量守恒定律可得W=![]() +
+![]() =
=![]() +
+![]()
代入数据解得W=0.4J;
(2)根据图象可知,图象与坐标轴围成的面积表示力F在t0时间内的冲量I,
则I=![]()
根据动量定理可得I-B![]() Lt0=mv-0
Lt0=mv-0
该过程中电容器所带的电荷量Q=![]() t0=CE=CBLv
t0=CE=CBLv
联立解得t0=1s。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目