题目内容
【题目】如图所示,在光滑水平面上,一个质量为m、速度大小为v的A球与质量为2m、静止的B球碰撞后,A球的速度方向与碰撞前相反。则碰撞后B球的速度大小可能是
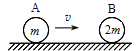
A. 0.40 v B. 0.55 v C. 0.60 v D. 0.70 v
【答案】BC
【解析】
首先从水平面光滑上判断AB两球碰撞过程中动量守恒,由于A球被反弹,所以可以判断出B球的速度会大于0.5v;在两球碰撞的过程中,有可能会存在能量的损失,由碰撞前后的动能求出B球的速度同时会小于等于![]() v,由两个速度的范围求出最终的结果。
v,由两个速度的范围求出最终的结果。
A球和B球碰撞的过程中动量守恒,设A、B两球碰撞后的速度分别为v1、v2,选A原来的运动方向为正方向,由动量守恒定律有:mv=-mv1+2mv2
假设碰后A球静止,即v1=0,可得:v2=0.5v
由题意知球A被反弹,所以球B的速度:v2>0.5v
AB两球碰撞过程能量可能有损失,由能量关系有![]() mv2≥
mv2≥![]() mv12+
mv12+![]() ×2mv22
×2mv22
两式联立得:v2≤![]() v
v
联立两式可得:0.5v<v2≤![]() v,故选BC。
v,故选BC。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目





