题目内容
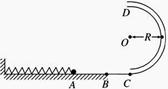
(19分)如图所示，足够长的光滑绝缘水平台左端固定一被压缩的绝缘轻质弹簧，一个质量
、电量
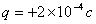的可视为质点的带电小球与弹簧接触但不栓接。某一瞬间释放弹簧弹出小球，小球从水平台右端A点飞出，恰好能没有碰撞地落到粗糙倾斜轨道的最高B点，并沿轨道滑下。已知AB的竖直高度
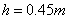，倾斜轨道与水平方向夹角为
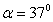、倾斜轨道长为
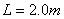，带电小球与倾斜轨道的动摩擦因数
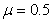。倾斜轨道通过光滑水平轨道CD与光滑竖直圆轨道相连，在C点没有能量损失，所有轨道都绝缘，运动过程小球的电量保持不变。只有过山车模型的竖直圆轨道处在范围足够大竖直向下的匀强电场中，场强
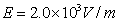。（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：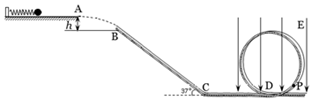
（1）被释放前弹簧的弹性势能？
（2）要使小球不离开轨道（水平轨道足够长），竖直圆弧轨道的半径应该满足什么条件？
（3）如果竖直圆弧轨道的半径
，小球进入轨道后可以有多少次通过竖直圆轨道上距水平轨道高为0.01m的某一点P？
（1）0.32J （2）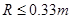
或
（3）6次通过距水平轨道高为0.01m的某一点
解析试题分析：（1）A到B平抛运动：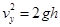
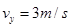1分
B点：
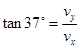
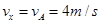2分
被释放前弹簧的弹性势能：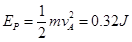
2分
（2）B点：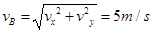
B到C：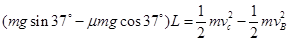
，
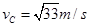2分
①恰好过竖直圆轨道最高点时：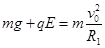
，
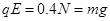
从C到圆轨道最高点：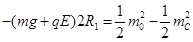
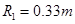2分
②恰好到竖直圆轨道最右端时：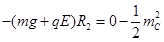
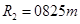2分
要使小球不离开轨道，竖直圆弧轨道的半径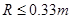或 2分
（3）
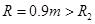，小球冲上圆轨道H1=0.825m高度时速度变为0，然后返回倾斜轨道h1高处再滑下，然后再次进入圆轨道达到的高度为H2。
有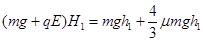
，
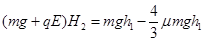2分
同除得：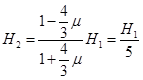
之后物块在竖直圆轨道和倾斜轨道之间往返运动
同理：n次上升高度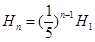
（n＞0）为一等比数列。 2分
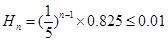，当n=4时，上升的最大高度小于0.01m
则小球共有6次通过距水平轨道高为0.01m的某一点。 2分
考点：本题考查平抛运动、动能定理、圆周运动
轻松夺冠全能掌控卷系列答案
探究能力是进行物理学研究的重要能力之一.物体因绕轴转动而具有的动能叫转动动能，转动动能的大小与物体转动的角速度有关.为了研究某一砂轮的转动动能Ek与角速度ω的关系，某同学采用了下述实验方法进行探索.如图所示，先让砂轮由动力带动匀速旋转，测得其角速度ω，然后让砂轮脱离动力，由于克服转轴间摩擦力做功，砂轮最后停下，测出砂轮脱离动力到停止转动的圈数n，通过分析实验数据得出结论.另外已测试砂轮转轴的直径为2 cm，转轴间的摩擦力为10 N/π.经实验测得的几组ω和n如下表所示:
| ω/rad·s-1 | 0.5 | 1 | 2 | 3 | 4 |
| n | 5.0 | 20 | 80 | 180 | 320 |
| Ek | | | | | |
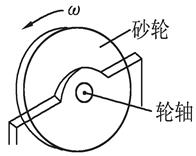
(1)计算出砂轮每次脱离动力的转动动能，并填入上表中.
(2)由上述数据推导出该砂轮的转动动能Ek与角速度ω的关系式为 .
(3)若测得脱离动力后砂轮的角速度为2.5 rad/s，则它转过45圈时的角速度为 rad/s 。
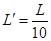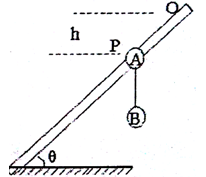
，高度差为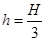
。若参赛者在运动过程中始终处于竖直状态，抓住滑轮的手与脚底之间的距离也为
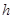，滑轮与钢丝绳间的摩擦力大小视为不变，且摩擦力所做功与滑过的路程成正比，不计参赛者在运动中受到的阻力、滑轮（含挂钩）的质量和大小，不考虑钢索桥的摆动及形变。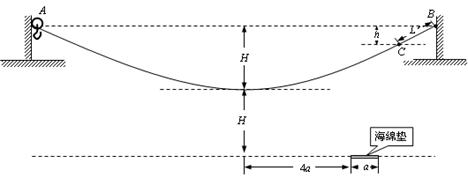
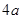、宽度为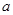
，厚度不计的海绵垫子上。若参赛者由A点静止滑下，会落在海绵垫子左侧的水中。为了能落到海绵垫子上，参赛者在A点抓住挂钩时应具有初动能的范围？
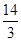倍。取g=10m/s2。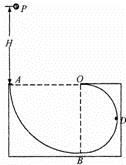
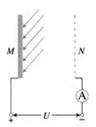
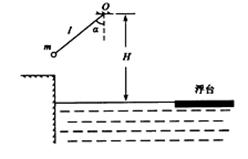
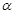=53o，绳的悬挂点O距水面的高度为H=3m.不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深。取重力加速度
， (
，
)
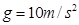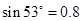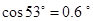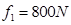，平均阻力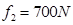
，求选手落入水中的深度
；