题目内容
如图所示，A、B两小球质量分别为mA=0.05kg、mB=0.lkg，用一根长为L=1.0rn的细绳连接，细绳是不能伸长的轻绳，A球套在一根斜放的粗糙杆上，杆与水平面夹角θ=300。起始，同时给A、B一个方向沿杆向下、大小相同的初速度，此后观察到A、B连线保持竖直。当A球运动到P点时，碰到钉子突然停下，B球继续运动，但沿绳方向的速度瞬间消失，只剩下垂直绳方向的速度，B球恰好能不与杆相碰，不计空气阻力，已知OP间的竖直高度为向h= l.0m，g取10m/s2，求：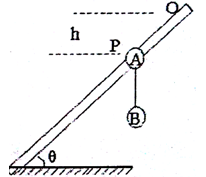
（1）A与杆接触面间的动摩擦因数μ。
（2）初速度v0的大小。
（3）整个过程中系统损失的机械能ΔE。
（1）
（2） （3）
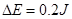
解析试题分析：（1）OP段，系统处于平衡状态，则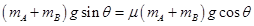
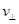
（2）A停止运动时，B以A为圆心沿切向一分速度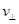摆起，法向分速度为
即时突变为零，如图所示，
则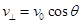
摆起过程，根据动能定理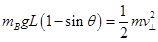
解得：
（3）根据能量守恒：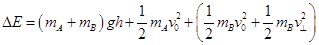
代入数据得：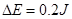
考点：本题考查动能定理、能量守恒，意在考查学生的综合分析能力。
练习册系列答案
相关题目
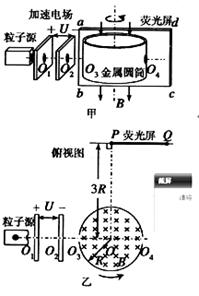
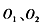为加速电场两极板上的小孔，
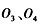为圆筒某一直径两端的小孔，abcd为竖直荧光屏，光屏与直线
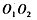平行。开始时
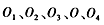在同一水平线上。已知加速电压为U，圆简半径为R，带正电的粒子质量为m，电量为q，圈筒转轴到光屏的距离OP＝3R（如图乙）。不计位子重力及粒子间相互作用。
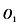进人电场时的速度可忽略，求粒子通过圆筒的时间to
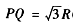（如图乙）。求粒子到达光屏时的速度大小v的范围，以及圆筒转动的角速度
。
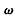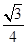×105 V/m，方向水平向右，Ⅲ区域磁感应强度B＝5.0 T，方向垂直纸面向里，三个区域宽度分别为d1＝5.0 m，d2＝4.0 m，d3＝
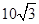m．一质量m＝1.0×10－8 kg、电荷量q＝1.6×10－6C的粒子从O点由静止释放，粒子重力忽略不计．求：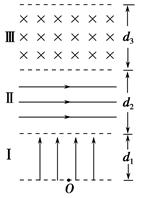
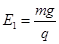，右侧空间有长为R＝0.114m的绝缘轻绳，绳的一端固定于O点，另一端拴一个质量为m小球B在竖直面内沿顺时针方向做圆周运动，运动到最低点时速度大小vB＝10m/s（小球B在最低点时与地面接触但无弹力）。在MN左侧水平面上有一质量也为m，带电量为
的小球A，某时刻在距MN平面L位置由静止释放，恰能与运动到最低点的B球发生正碰，并瞬间粘合成一个整体C。（取g＝10m/s2）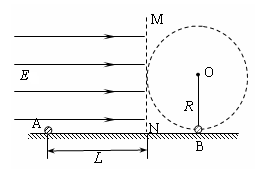
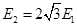，当L满足什么条件时，整体C可在竖直面内做完整的圆周运动。（结果保留1位小数）
，
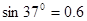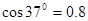，g取 l0m/s2．求： 
从a点出发，沿直线AB向b点运动，其中小滑块第一次经过O点时的动能为初动能的n倍（n>l），到达b点时动能恰好为零,小滑块最终停在O点，求：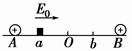
；
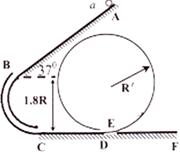
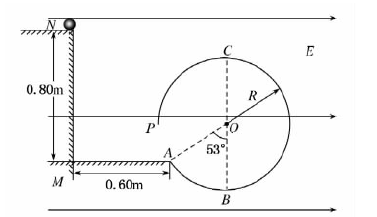
、电量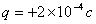
的可视为质点的带电小球与弹簧接触但不栓接。某一瞬间释放弹簧弹出小球，小球从水平台右端A点飞出，恰好能没有碰撞地落到粗糙倾斜轨道的最高B点，并沿轨道滑下。已知AB的竖直高度
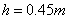，倾斜轨道与水平方向夹角为
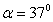、倾斜轨道长为
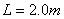，带电小球与倾斜轨道的动摩擦因数
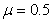。倾斜轨道通过光滑水平轨道CD与光滑竖直圆轨道相连，在C点没有能量损失，所有轨道都绝缘，运动过程小球的电量保持不变。只有过山车模型的竖直圆轨道处在范围足够大竖直向下的匀强电场中，场强
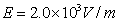。（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：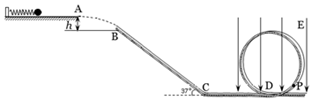
，小球进入轨道后可以有多少次通过竖直圆轨道上距水平轨道高为0.01m的某一点P？