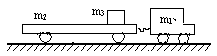
题目内容
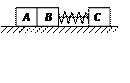
如图所示，质量为M的平板车的长度为L，左端放一质量为m的小物块，今使小物块与小车一起以共同速度v0沿光滑水平面向右运动，小车将与竖直墙发生弹性碰撞，而小物块最终又恰与小车相对静止于小车的最右端，求小物块与小车上表面间的动摩擦因数。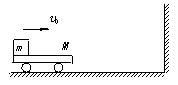
当m＜M时，
=
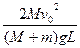；当m＞M时，=
。
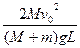=；当m＞M时，=。(1)当m＜M时，小车与竖直墙做弹性碰撞后小车和物体与小物体分别以速率v0向左向右运动，最后共同速度为v
Mv0－mv0=(M＋m)v?
mgL=
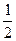(M＋m)v02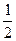－ (M＋m)v2?
解得:=
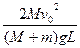
(2)当m＞M时, 小车与竖直墙第一次弹性碰撞后分别以v0向左、向右运动.
p物＞p车. 相对静止时速度为v,方向向右, 发生第二次弹性碰撞, 多次往复运动, 最终小车与物块将静止, 则
mgL=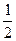(m＋M)v02
=
Mv0－mv0=(M＋m)v?
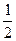mgL=(M＋m)v02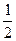－ (M＋m)v2?解得:
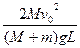
=(2)当m＞M时, 小车与竖直墙第一次弹性碰撞后分别以v0向左、向右运动.
p物＞p车. 相对静止时速度为v,方向向右, 发生第二次弹性碰撞, 多次往复运动, 最终小车与物块将静止, 则
mgL=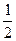(m＋M)v02=
练习册系列答案
阅读快车系列答案
相关题目
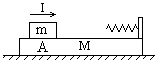
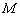的木块在光滑水平面上以速度
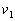向右运动，质量为
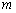的子弹以速度
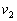水平向左射入木块，要使木块停下来，必须发射的子弹数目为（子弹留在木块中不穿出）：（ ）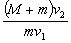
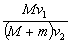
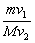
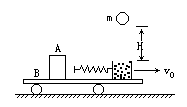
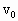向右匀速运动，物块A与其左侧的车面的动摩擦因数为
，与其余部分车面间无摩擦．在车匀速运动时，距沙面H高处有一质量为m的泥球自由下落，恰好落在沙箱中，试求：
