题目内容
如图所示,在光滑水平地面上静放着质量为m=2Kg的小滑块和质量为M=4Kg、长L=8m的薄板。滑块和薄板间动摩擦因数为μ=0.2,且最大静摩擦力等于滑动摩擦力。若向薄板施加水平拉力F=20N,作用2s后撤去,取g=10m/s2。求:
(1)拉力F所做的功。
(2)薄板在水平地面上运动的最终速度。
(1)拉力F所做的功。
(2)薄板在水平地面上运动的最终速度。

(1)160J(2)
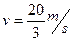
(1)由牛顿第二定律可得:二者要发生相对运动
滑块的加速度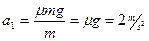 (1分)
(1分)
薄板的加速度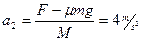 (1分)
(1分)
若薄板足够长,2s时二者对地位移分别为:
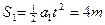 (1分)
(1分) 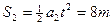 (1分)
(1分)
两者的相对位移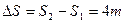 <L (1分) 说明此时滑块没有脱离薄板
<L (1分) 说明此时滑块没有脱离薄板
所以拉力做的功为: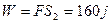 (2分)
(2分)
(2)力F撤消瞬间,两者的速度分别为: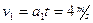 (1分)
(1分) 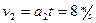 (1分)
(1分)
若薄板足够长,则二者最终共速为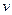 ,由动量及能量守恒定律可得:
,由动量及能量守恒定律可得:
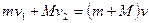 (2分)
(2分)
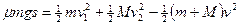 (2分)
(2分)
代入数字解得: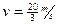 (1分)
(1分) 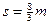 <
<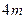 (滑块没有离开薄板)(1分)
(滑块没有离开薄板)(1分)
所以二者最终共速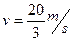 (1分)
(1分)
滑块的加速度
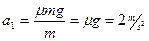 (1分)
(1分)薄板的加速度
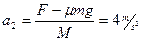 (1分)
(1分)若薄板足够长,2s时二者对地位移分别为:
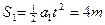 (1分)
(1分) 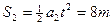 (1分)
(1分) 两者的相对位移
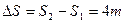 <L (1分) 说明此时滑块没有脱离薄板
<L (1分) 说明此时滑块没有脱离薄板 所以拉力做的功为:
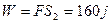 (2分)
(2分)(2)力F撤消瞬间,两者的速度分别为:
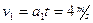 (1分)
(1分) 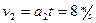 (1分)
(1分)若薄板足够长,则二者最终共速为
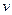 ,由动量及能量守恒定律可得:
,由动量及能量守恒定律可得: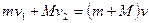 (2分)
(2分)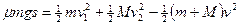 (2分)
(2分)代入数字解得:
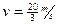 (1分)
(1分) 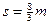 <
<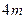 (滑块没有离开薄板)(1分)
(滑块没有离开薄板)(1分)所以二者最终共速
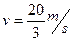 (1分)
(1分)
练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
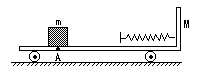
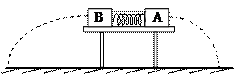
 =6m/s的初速度在平板上滑行,与固定在平板车上的弹簧作用后又弹回,最后刚好回到A点与车保持相对静止,在此过程中小滑块相对于小车通过的总路程s=3m,g=10
=6m/s的初速度在平板上滑行,与固定在平板车上的弹簧作用后又弹回,最后刚好回到A点与车保持相对静止,在此过程中小滑块相对于小车通过的总路程s=3m,g=10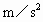 ,试求:
,试求: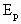 ;
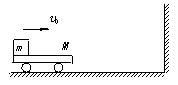
;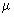 .
.
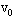 =800m/s射入木块后留在木块中,当木块与前方距离较远的竖直墙碰后,以4m/s的速度反弹回,木块与墙的作用时间为0.1s
=800m/s射入木块后留在木块中,当木块与前方距离较远的竖直墙碰后,以4m/s的速度反弹回,木块与墙的作用时间为0.1s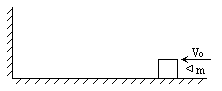
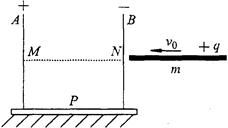
 光滑圆弧的质量为M的曲面体,已知曲面顶端切线竖直。若M未能越过曲面体,求球到达最高点时曲面体的速度以及曲面半径的最小值。
光滑圆弧的质量为M的曲面体,已知曲面顶端切线竖直。若M未能越过曲面体,求球到达最高点时曲面体的速度以及曲面半径的最小值。
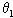 =37°的光滑斜面 AB 与倾角
=37°的光滑斜面 AB 与倾角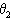 =30°的光滑斜面 DC,通过长度为 2.2m 的光滑水平面 BC 连接(连接处有一段很短的光滑圆弧),将质量
=30°的光滑斜面 DC,通过长度为 2.2m 的光滑水平面 BC 连接(连接处有一段很短的光滑圆弧),将质量 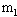 ="0.5kg" 的小球 P 从 AB 斜面上距地高度
="0.5kg" 的小球 P 从 AB 斜面上距地高度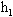 ="1.8m" 处自由释放,同时将质量为
="1.8m" 处自由释放,同时将质量为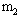 的另一小球Q从DC面上某点释放.要使小球同时进入水平面,且不断地在水平面上同一点发生相向碰撞(机械能无损失).求:
的另一小球Q从DC面上某点释放.要使小球同时进入水平面,且不断地在水平面上同一点发生相向碰撞(机械能无损失).求: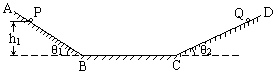
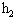 是多少?
是多少?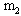 是多少?
是多少?
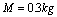 的木块(可视为质点),在木块正上方1m处有一固定的悬点O,在悬点O和木块之间用一根长2m、不可伸长的轻绳连接。有一颗质量m=0.1kg的子弹以80m/s的速度射入木块并留在其中,之后木块绕O点在竖直平面内做圆周运动。
的木块(可视为质点),在木块正上方1m处有一固定的悬点O,在悬点O和木块之间用一根长2m、不可伸长的轻绳连接。有一颗质量m=0.1kg的子弹以80m/s的速度射入木块并留在其中,之后木块绕O点在竖直平面内做圆周运动。