题目内容
跨过定滑轮的绳的一端挂一吊板,另一端被吊板上的人拉住,如图所示.已知人的质量为50kg,吊板的质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计.取重力加速度g=10m/s2.当人以360N的力拉绳时,人与吊板的加速度a和人对吊板的压力F分别为

A.a=1.0m/s2,F=260N
B.a=2.4m/s2,F=236N
C.a=3.0m/s2,F=140N
D.a=2.0m/s2,F=240N
【答案】
D
【解析】
试题分析:以人与吊板整体为研究对象,根据牛顿第二定律得:
2T-(M+m)g=(M+m)a,解得:a=2m/s2
再对吊板研究,则有:T-(mg+F)=ma,得到:F=T-ma-mg=360N-10×12N=240N
故选D.
考点:牛顿定律及整体法隔离法问题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
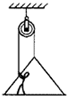 跨过定滑轮的绳的一端挂一吊板,另一端被吊板上的人拉住,如图所示.已知人的质量为50kg,吊板的质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计.取重力加速度g=10m/s2.当人以360N的力拉绳时,人与吊板的加速度a和人对吊板的压力F分别为( )
跨过定滑轮的绳的一端挂一吊板,另一端被吊板上的人拉住,如图所示.已知人的质量为50kg,吊板的质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计.取重力加速度g=10m/s2.当人以360N的力拉绳时,人与吊板的加速度a和人对吊板的压力F分别为( )| A、a=1.0m/s2,F=260N | B、a=2.4m/s2,F=236N | C、a=3.0m/s2,F=140N | D、a=2.0m/s2,F=240N |
 (2002?河南)跨过定滑轮的绳的一端挂一吊板,另一端被吊板上的人拉住,如图所示.已知人的质量为70kg,吊板的质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计.取重力加速度g=10m/s2.当人以440N的力拉绳时,人与吊板的加速度a和人对吊板的压力F分别为( )
(2002?河南)跨过定滑轮的绳的一端挂一吊板,另一端被吊板上的人拉住,如图所示.已知人的质量为70kg,吊板的质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计.取重力加速度g=10m/s2.当人以440N的力拉绳时,人与吊板的加速度a和人对吊板的压力F分别为( ) 跨过定滑轮的绳的一端挂一吊板,另一端被吊板上的人拉住,如图所示,已知人的质量为70kg,吊板的质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计.取重力加速度g=10m/s2,当人以440N的力拉绳时,人对吊板的压力为
跨过定滑轮的绳的一端挂一吊板,另一端被吊板上的人拉住,如图所示,已知人的质量为70kg,吊板的质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计.取重力加速度g=10m/s2,当人以440N的力拉绳时,人对吊板的压力为 跨过定滑轮的绳的一端挂一吊板,另一端被吊板上的人拉住,如图所示,已知人的质量为70kg,吊板的质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计,取重力加速度g=10m/s2.当人以440N的力拉绳时,人与吊板的加速度a和人对吊板的压力F分别为( )
跨过定滑轮的绳的一端挂一吊板,另一端被吊板上的人拉住,如图所示,已知人的质量为70kg,吊板的质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计,取重力加速度g=10m/s2.当人以440N的力拉绳时,人与吊板的加速度a和人对吊板的压力F分别为( ) 如图所示,跨过定滑轮的绳的一端挂一吊板,另一端被吊板上的人拉住,已知人的质量为70kg,吊板的质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计,取重力加速度g=10m/s2.当人以440N的力拉绳时,人与吊板的加速度a和人对吊板的压力F分别为多少?
如图所示,跨过定滑轮的绳的一端挂一吊板,另一端被吊板上的人拉住,已知人的质量为70kg,吊板的质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计,取重力加速度g=10m/s2.当人以440N的力拉绳时,人与吊板的加速度a和人对吊板的压力F分别为多少?