题目内容
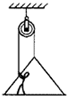跨过定滑轮的绳的一端挂一吊板，另一端被吊板上的人拉住，如图所示．已知人的质量为50kg，吊板的质量为10kg，绳及定滑轮的质量、滑轮的摩擦均可不计．取重力加速度g=10m/s2．当人以360N的力拉绳时，人与吊板的加速度a和人对吊板的压力F分别为（ ）| A、a=1.0m/s2，F=260N | B、a=2.4m/s2，F=236N | C、a=3.0m/s2，F=140N | D、a=2.0m/s2，F=240N |
分析：先以人与吊板整体为研究对象，根据牛顿第二定律求出加速度，再对吊板进行研究，再由牛顿第二定律求出人对吊板的压力F．
解答：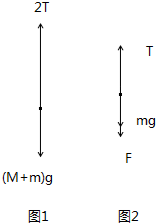
解：以人与吊板整体为研究对象，受力如图1所示，根据牛顿第二定律得：
加速度a=
m/s2=
m/s2=2.0m/s2
再对吊板研究，受力如图2所示，则有：T-（mg+F）=ma，
得到：F=T-ma-mg=360-10×2-10×10=240N
故选：D．
解：以人与吊板整体为研究对象，受力如图1所示，根据牛顿第二定律得：加速度a=
| 2T-(M+m)g |
| M+m |
| 360×2-(60+10)×10 |
| 60+10 |
再对吊板研究，受力如图2所示，则有：T-（mg+F）=ma，
得到：F=T-ma-mg=360-10×2-10×10=240N
故选：D．
点评：本题是连接体类型的问题，抓住吊板与人加速度相同，运用整体法和隔离法相结合进行处理．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
（2002?河南）跨过定滑轮的绳的一端挂一吊板，另一端被吊板上的人拉住，如图所示．已知人的质量为70kg，吊板的质量为10kg，绳及定滑轮的质量、滑轮的摩擦均可不计．取重力加速度g=10m/s2．当人以440N的力拉绳时，人与吊板的加速度a和人对吊板的压力F分别为（ ）
跨过定滑轮的绳的一端挂一吊板，另一端被吊板上的人拉住，如图所示，已知人的质量为70kg，吊板的质量为10kg，绳及定滑轮的质量、滑轮的摩擦均可不计．取重力加速度g=10m/s2，当人以440N的力拉绳时，人对吊板的压力为
跨过定滑轮的绳的一端挂一吊板，另一端被吊板上的人拉住，如图所示，已知人的质量为70kg，吊板的质量为10kg，绳及定滑轮的质量、滑轮的摩擦均可不计，取重力加速度g=10m/s2．当人以440N的力拉绳时，人与吊板的加速度a和人对吊板的压力F分别为（ ）
如图所示，跨过定滑轮的绳的一端挂一吊板，另一端被吊板上的人拉住，已知人的质量为70kg，吊板的质量为10kg，绳及定滑轮的质量、滑轮的摩擦均可不计，取重力加速度g=10m/s2．当人以440N的力拉绳时，人与吊板的加速度a和人对吊板的压力F分别为多少？