题目内容
某研究性学习小组首先根据小孔成像原理估测太阳半径，再利用万有引力定律估算太阳的密度.准备的器材有:①不透光圆筒，一端封上不透光的厚纸，其中心扎一小孔，另一端封上透光的薄纸；②毫米刻度尺.已知地球绕太阳公转的周期为T，万有引力常量为G。要求:（1）简述根据小孔成像原理估测太阳半径R的过程。（2）利用万有引力定律推算太阳密度。
⑴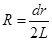
⑵
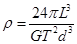
解析试题分析：⑴ 其过程如图所示，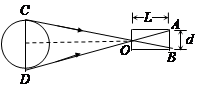
用不透光圆筒，把有小孔的一端对准太阳，调节圆筒到太阳的距离，在薄纸的另一端可以看到太阳的像.用毫米刻度尺测得太阳像的直径d，圆筒长为L.成像光路图（2分）
设太阳的半径为R，太阳到地球的距离为r.由成像光路图可知:△ABO∽△CDO，则: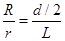
，即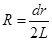. （2分）
（2）地球绕太阳做匀速圆周运动，万有引力提供向心力，设太阳质量为M，地球质量为m，则: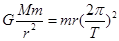
（2分）
由密度公式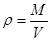
及球体体积公式
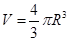（2分）
联立以上各式可得: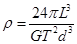 （1分）
考点：本题考查数学知识在物理中的应用、万有引力定律。
练习册系列答案
相关题目
经长期观测人们在宇宙中已经发现了“双星系统”．“双星系统”是由两颗相距较近的恒星组成，每个恒星的线度远小于两个星体之间的距离，而且双星系统一般远离其他天体．如右图所示，两颗星球组成的双星，在相互之间的万有引力的作用下，绕连线上的O点做周期相同的匀速圆周运动．现测得两颗星之间的距离为L，质量之比为m1∶m2＝3∶2.则可知( )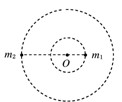
| A．m1、m2做圆周运动的线速度之比为3∶2 |
| B．m1、m2做圆周运动的角速度之比为3∶2 |
C．m1做圆周运动的半径为 |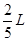
| D．m2做圆周运动的半径为 |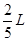
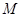，半径为
，万有引力常量为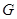
．请你结合以上数据求：
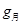； ②月球的第一宇宙速度
；