题目内容
相隔一定距离的A,B两球质量相等,假定它们之间存在恒定的斥力作用.原来两球被按住,处在静止状态.现突然松开两球,同时给A球以速度v0,使之沿两球连线射向B球,B球初速为零.若两球间的距离从最小值(两球未接触)到刚恢复到原始值所经历的时间为t0.求B球在斥力作用下的加速度.
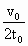
以m表示每个球的质量,F表示恒定斥力,L表示两球间原始距离,松开后,A球做初速为v0的匀减速运动,B球做初速为零的匀加速运动.设在两球间距由L变小到恢复到L的过程中,A球的路程为L1,B球的路程为L2;刚恢复到原始长度时,A球的速度为v1,B球的速度为v2.由动量守恒定律有mv0=mv1+mv2.由功能关系得FL1=
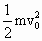 -
-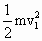 ,FL2=
,FL2=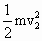 .由于初、末态两球间距相等,故有L1=L2,由以上各式解得v2=v0.当两球速度相等时,距离最小,设此时球速为u,由动量守恒定律得mv0=(m+m)u,设a为B球的加速度,则有v2=u+at0,得a=
.由于初、末态两球间距相等,故有L1=L2,由以上各式解得v2=v0.当两球速度相等时,距离最小,设此时球速为u,由动量守恒定律得mv0=(m+m)u,设a为B球的加速度,则有v2=u+at0,得a=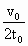 .
.
练习册系列答案
相关题目



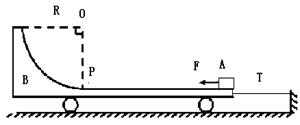 如图所示,水平光滑地面上停放着一辆小车B,其质量为M=4Kg,右端用细绳T系在墙上,小车的四分之一圆弧轨道半径为R=1.7m,在最低点P处与长为L=2m的水平轨道相切,可视为质点的质量为m=2Kg物块A放在小车B的最右端,A与B的动摩擦因数为μ=0.4,整个轨道处于同一竖直平面内。现对A施加向左的水平恒力F=48.5N,当A运动到P点时,撤去F,同时剪断细绳,物块恰好能到达圆弧的最高点,当其再次返回P点时,动能为第一次过P点时的
如图所示,水平光滑地面上停放着一辆小车B,其质量为M=4Kg,右端用细绳T系在墙上,小车的四分之一圆弧轨道半径为R=1.7m,在最低点P处与长为L=2m的水平轨道相切,可视为质点的质量为m=2Kg物块A放在小车B的最右端,A与B的动摩擦因数为μ=0.4,整个轨道处于同一竖直平面内。现对A施加向左的水平恒力F=48.5N,当A运动到P点时,撤去F,同时剪断细绳,物块恰好能到达圆弧的最高点,当其再次返回P点时,动能为第一次过P点时的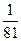 。取g=10m/s2。求
。取g=10m/s2。求
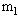 =0.2kg、
=0.2kg、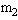 =0.6kg,用细线系住并压缩一个轻质弹簧,铁块与左侧墙的距离是8.0m(如图).现将细线烧断,小铁块在弹簧弹力作用下,沿垂直于墙的直线反向运动,铁块与水平地面间的动摩擦因数为μ=0.1.m1与墙相碰后返回追
=0.6kg,用细线系住并压缩一个轻质弹簧,铁块与左侧墙的距离是8.0m(如图).现将细线烧断,小铁块在弹簧弹力作用下,沿垂直于墙的直线反向运动,铁块与水平地面间的动摩擦因数为μ=0.1.m1与墙相碰后返回追
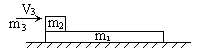
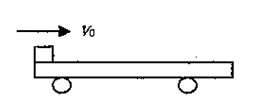
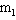 、长为L的木板,在其左端放一质量为
、长为L的木板,在其左端放一质量为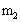 可视为质点的木块,有一颗质量为
可视为质点的木块,有一颗质量为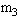 的子弹以
的子弹以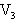 射入木块,射穿木块后子弹速度减小到
射入木块,射穿木块后子弹速度减小到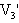 。问木块与木板的动摩擦因数为多大时,木块才不致于从木板上滑出?(子弹穿过木块的时间极短,可以忽略)
。问木块与木板的动摩擦因数为多大时,木块才不致于从木板上滑出?(子弹穿过木块的时间极短,可以忽略)