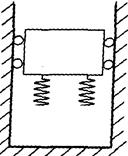
题目内容
如图所示，一个线轴质量为m，边缘轮半径为R ，中间轴半径为r，一根细线一端固定在轴上最低点C处，然后在轴上沿顺时针方向绕了两周。线轴放在水平桌面上，它与桌面间的动摩擦因数为μ。现用水平外力F向左慢慢拉细线的另一端，直到绕在线轴上的细线全部松开，这时线轴的C点又位于最低点，并且C点的位移恰好等于中心轴周长的2倍。求这个过程中产生的热量是多大？
2πμmg(r+R)
假设线轴从起始位置先向右纯滚两周，至C点又位于最低点，绳端松开长度为s1=2πr，而线轴后退距离为s2=2πR，。此过程中线轴与水平桌面间没有滑动摩擦。
再使线轴沿水平桌面向右平动，在桌面上滑行至题目要求的位置，线轴在桌面上滑行的距离等于s= s1+s2=2π（r+R）。所生的热量等于滑动摩擦力与相对运动的路程的乘积，即
Q=f·s=2πμmg(r+R)。
练习册系列答案
相关题目
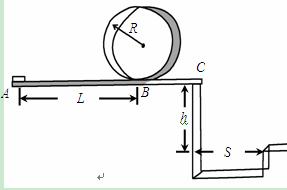
的平板B左端, B放在水平面上, A、B两物体通过一个动滑轮相连, 动滑轮固定在墙上, 滑轮的质量及摩擦不计, A的质量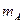
=1.0kg
, B的质量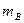
= 3.0kg , A、B之间及B与水平面的动摩擦因数m= 0.25, 现用一个水平向左的恒力F拉B, 经t= 2.0s后A滑离B, 求拉力F的大小. (取g =10m/s2 ) 
与弹簧的形变量x之间的关系为
，于是他们设想，让弹簧的弹性势能全部释放出来推动物体沿不光滑的水平面运动，测量对应弹簧不同压缩量下物体滑行的距离，就可以定性地验证这一结论，他们设计了如下实验：将带有挡板的表面处处粗糙程度相同的木板固定在水平桌面上，将一根很轻的弹簧(约14cm),一端固定在挡板上，将一个做有标记的物块紧贴弹簧放置在弹簧原长处，并在木板侧面平行木板固定一长条硬纸板，将物块的标记位置记录在纸板上，记作O，并以O为坐标原点，以平行木板方向建立x轴，在x轴上O 点的左侧用刻度尺自O点向左每间隔1cm做出刻度线，记作x0=-1cm、-2cm。并将刻度尺固平行固定在木板侧面，并使其0雇刻线与O点重合，在进行实验时，使弹簧的压缩量以1cm递增，释放物块，并记录物块最终停止运动时标记所在的位置，用刻度尺测量出该位置距离O点的距离，记作x1，记录的数据如图所示；
