题目内容
8. 如图所示,点光源S到平面镜M的距离为d=0.5m.光屏AB与平面镜的初始位置平行.当平面镜M绕垂直于纸面过中心O的转轴以ω=4rad/s的角速度逆时针匀速转过300时,垂直射向平面镜的光线SO在光屏上的光斑P的移动速度大小是多少?
如图所示,点光源S到平面镜M的距离为d=0.5m.光屏AB与平面镜的初始位置平行.当平面镜M绕垂直于纸面过中心O的转轴以ω=4rad/s的角速度逆时针匀速转过300时,垂直射向平面镜的光线SO在光屏上的光斑P的移动速度大小是多少?
分析 当平面镜转动θ=30°角时,由光的反射定律可得,反射光线转动2θ角度;根据运动的合成与分解,及圆周运动的角速度与半径的关系,即可求解
解答  解 设平面镜转过30°角时,光线反射到光屏上的光斑P点,光斑速度为v,由图可知:
解 设平面镜转过30°角时,光线反射到光屏上的光斑P点,光斑速度为v,由图可知:
v=$\frac{{v}_{⊥}}{cos2θ}$,
而 v⊥=l•2ω=$\frac{d}{cos2θ}$•2ω,
故 v=$\frac{2ωd}{co{s}^{2}2θ}$=8ωd,
答:垂直射向平面镜的光线SO在光屏上的光斑P的移动速度大小为8ωd.
点评 本题考查光的反射定律,掌握运动的合成与分解,理解角速度与半径的关系,并结合几何关系解答.

练习册系列答案
相关题目
20. 家用电热灭蚊器电热部分的主要器件是PCT元件,PCT元件是由钛酸钡等导体材料制成的电阻器,其电阻率ρ与温度t的关系如图所示.由于这种特性,PCT元件具有发热、控温双重功能.对此,以下判断中正确的是( )
家用电热灭蚊器电热部分的主要器件是PCT元件,PCT元件是由钛酸钡等导体材料制成的电阻器,其电阻率ρ与温度t的关系如图所示.由于这种特性,PCT元件具有发热、控温双重功能.对此,以下判断中正确的是( )
 家用电热灭蚊器电热部分的主要器件是PCT元件,PCT元件是由钛酸钡等导体材料制成的电阻器,其电阻率ρ与温度t的关系如图所示.由于这种特性,PCT元件具有发热、控温双重功能.对此,以下判断中正确的是( )
家用电热灭蚊器电热部分的主要器件是PCT元件,PCT元件是由钛酸钡等导体材料制成的电阻器,其电阻率ρ与温度t的关系如图所示.由于这种特性,PCT元件具有发热、控温双重功能.对此,以下判断中正确的是( )| A. | 通电后,其电功率先增大后减小 | |
| B. | 通电后,其电功率先减小后增大 | |
| C. | 当其产生的热量与散发的热量相等时,温度保持在t1或t2不变 | |
| D. | 当其产生的热量与散发的热量相等时,温度保持在t1至t2间的某一值不变 |
17.一定质量的理想气体自状态A经状态B变化到状态C,这个一过程在V-T图中的表示如图所示,则下列说法错误的是( )


| A. | 在过程AB中,气体压强不断变大 | B. | 在过程BC中,气体密度不断变大 | ||
| C. | 在过程AB中,气体对外界做功 | D. | 在过程BC中,外界对气体做功 |
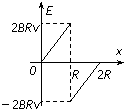
 如图所示,xOy平面内有一半径为R的圆形区域,区域内有磁感应强度大小为B的匀强磁场,左半圆磁场方向垂直于xOy平面向里,右半圆磁场方向垂直于xOy平面向外.一平行于y轴的长导体棒ab以速度v沿x轴正方向做匀速运动,则导体棒ab两端的感应电动势E(取b点电势高时为正)与导体棒位置x关系的图象是( )
如图所示,xOy平面内有一半径为R的圆形区域,区域内有磁感应强度大小为B的匀强磁场,左半圆磁场方向垂直于xOy平面向里,右半圆磁场方向垂直于xOy平面向外.一平行于y轴的长导体棒ab以速度v沿x轴正方向做匀速运动,则导体棒ab两端的感应电动势E(取b点电势高时为正)与导体棒位置x关系的图象是( )


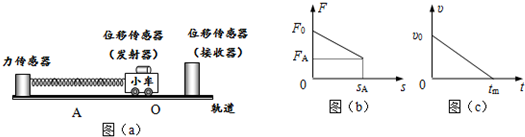


 某兴趣小组查阅资料获知,弹簧振子做简谐运动的周期T=2π$\sqrt{\frac{m}{k}}$(其中m是振子的质量,k是弹簧的劲度系数,弹簧质量忽略不计),利用该规律可以测定物体的质量.现有如下器材可供选择:
某兴趣小组查阅资料获知,弹簧振子做简谐运动的周期T=2π$\sqrt{\frac{m}{k}}$(其中m是振子的质量,k是弹簧的劲度系数,弹簧质量忽略不计),利用该规律可以测定物体的质量.现有如下器材可供选择: 一台直流电动机线圈电阻r=1Ω,与一阻值R=10Ω的电阻串联,当所加电压U=150V,电动机正常工作时电压表示数100V,求电动机消耗的功率及输出的机械功率.
一台直流电动机线圈电阻r=1Ω,与一阻值R=10Ω的电阻串联,当所加电压U=150V,电动机正常工作时电压表示数100V,求电动机消耗的功率及输出的机械功率.