题目内容
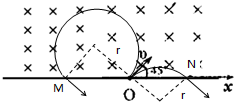
如图所示,在x轴上方存在磁感应强度为B的匀强磁场,一对正、负电子(质量m,电荷量为e)从x轴上的O点以速度v斜向上射入磁场中,速度方向与x轴的夹角为45°并与磁场方向垂直.正电子在磁场中运动一段时间后,从x轴上的M点射出磁场.负电子在磁场中运动一段时间后,从x轴上的N点射出磁场.求:
(1)画出正、负电子的运动轨迹,在x轴上标出M、N的位置
(2)MN两点间的距离
(3)正电子在磁场中运动的时间.

(1)画出正、负电子的运动轨迹,在x轴上标出M、N的位置
(2)MN两点间的距离
(3)正电子在磁场中运动的时间.

(1)根据左手定则判断可知,正电子所受的洛伦兹力垂直于v向上,负电子所受的洛伦兹力垂直于v向下,它们的运动轨迹如图所示.
(2)设电子的轨迹半径为r.
由牛顿第二定律得:
evB=m
| v2 |
| r |
解得:r=
| mv |
| eB |
由几何关系得:MN=2
| 2 |
2
| ||
| eB |
(3)电子的运动周期为 T=
| 2πr |
| v |
| 2πm |
| Be |
如左侧正电子的轨迹所示,正电子轨迹对应的圆心角为270°,则正电子在磁场中运动的时间为:
t=
| 3 |
| 4 |
| 3πm |
| 2Be |
答:
(1)画出正、负电子的运动轨迹见上,在x轴上标出M、N的位置见上.
(2)MN两点间的距离为
2
| ||
| eB |
(3)正电子在磁场中运动的时间为
| 3πm |
| 2Be |

练习册系列答案
相关题目







