题目内容
如图所示的坐标平面内，在Y＜0的区域内存在着垂直纸面向外的匀强磁场，在Y＞0的区域内存在着与X轴正方向成45°角的匀强电场，电场强度E=2N/C．一比荷
=1.0×l08C/kg的带负电的粒子从坐标原点O沿与X负方向成45°角射入第三象限，速度大小v0=2.0×104m/s，先后在磁场和电场中运动一段时间后粒子能再次通过O点，试求：
（1）匀强磁场的磁感应强度B
（2）粒子从O点发射到再次回到O点所用的时间．
| q |
| m |
（1）匀强磁场的磁感应强度B
（2）粒子从O点发射到再次回到O点所用的时间．
（1）如图，带电粒子自P点进入电场，到o点的偏转角为45°，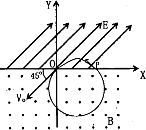
tan45°=
a=
解得：t1=
=2×2×104×
×
=2.0×10-4s
OP=
v0t1=4
m
由几何关系可知粒子在磁场中运动半径为r=4m，
由qvB=m
代入数据解得B=5×10-5T
（2）带电粒子在磁场中运动
个圆周，t2=
T=
=3π×10-4s
粒子从O点发射到再次回到O点所用的时间：t=t1+t2=（2+3π）×10-4s
答：（1）磁感应强度的大小5×10-5T；
（2）粒子从O点发射到再次回到O点所用的时间为（2+3π）×10-4s
tan45°=
| ||
| v0t1 |
a=
| Eq |
| m |
解得：t1=
| 2mv0 |
| Eq |
| 1 |
| 1.0×108 |
| 1 |
| 2 |
OP=
| 2 |
| 2 |
由几何关系可知粒子在磁场中运动半径为r=4m，
由qvB=m
| v2 |
| R |
代入数据解得B=5×10-5T
（2）带电粒子在磁场中运动
| 3 |
| 4 |
| 3 |
| 4 |
| 3πm |
| 2Bq |
粒子从O点发射到再次回到O点所用的时间：t=t1+t2=（2+3π）×10-4s
答：（1）磁感应强度的大小5×10-5T；
（2）粒子从O点发射到再次回到O点所用的时间为（2+3π）×10-4s
练习册系列答案
相关题目
、电荷量为
的粒子(重力不计)，粒子从
孔漂进(初速不计)一个水平方向的加速电场，再经小孔
进入相互正交的匀强电场和匀强磁场区域，电场强度大小为
，磁感应强度大小为
，方向如图．虚线PQ、MN之间存在着水平向右的匀强磁场，磁感应强度大小为
(图中未画出)．有一块折成直角的硬质塑料板abc(不带电，宽度很窄，厚度不计)放置在PQ、MN之间(截面图如图)，
、
两点恰在分别位于PQ、MN上，
，
，现使粒子能沿图中虚线
进入PQ、MN之间的区域，求：
；
