题目内容
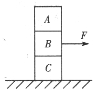
【题目】如图所示，在倾角为θ的斜面上，轻质弹簧一端与斜面底端固定，另一端与质量为M的平板A连接，一个质量为m的物体B靠在平板的右侧，A、B与斜面的动摩擦因数均为μ．开始时用手按住物体B使弹簧处于压缩状态，现放手，使A和B一起沿斜面向上运动距离L时，A和B达到最大速度v．则以下说法正确的是（ ）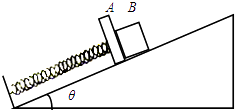
A.A和B达到最大速度v时，弹簧是自然长度
B.若运动过程中A和B能够分离，则A和B恰好分离时，二者加速度大小均为g（sinθ+μcosθ ）
C.从释放到A和B达到最大速度v的过程中．弹簧对A所做的功等于 
mv2+MgLsinθ+μMgLcosθ
D.从释放到A和B达到最大速度v的过程中，B受到的合力对它做的功大于 mv2
【答案】B
【解析】解：A：对物体B和平板A整体分析可知，A和B达到最大速度时应满足kx=（m+M）gsinθ+μ（m+M）gcosθ，说明弹簧仍处于压缩状态，所以A错误；
B：根据题意可知，A和B恰好分离时，弹簧正好恢复原长，对A和B整体由牛顿第二定律得：
（m+M）gsinθ+μ（m+M）gcosθ=（m+M）a，
解得：a=gsinθ+μgcosθ=g（sinθ+μcosθ），所以B正确；
C：对A从释放到速度达到最大的过程由动能定理可得：W弹﹣Mg（xm﹣x）sinθ﹣μMg（xm﹣x）cosθ﹣FN（xm﹣x）= 
Mv2，
其中xm是弹簧压缩的最大长度，x是速度最大时弹簧压缩的长度，FN是B对A的压力大小，比较可知C错误；
D：对B从释放到A和B达到最大速度的过程由动能定理可得：W总= 
﹣0，即B受到的合力对它做的功等于 ，所以D错误；
故选：B．
【考点精析】根据题目的已知条件，利用动能定理的综合应用的相关知识可以得到问题的答案，需要掌握应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷．
