题目内容
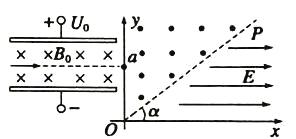
【题目】如图所示，一半径为R的竖直光滑圆轨道固定在倾角为37°的静止斜面上，圆轨道与斜面相切于N点，MN为圆轨道的直径。一个质量为m的小球恰好能在圆轨道内侧做圆周运动。重力加速度为g，sin37°=0.6，cos37°=0.8。则
A. 小球过M点时的速度等于
B. 小球过M点时的速度大于
C. 小球从M点运动到N点过程中重力势能变化量为2mgR
D. 小球从M点运动到N焦过程中重力势能变化量为
【答案】BD
【解析】试题小球通过轨道最高点时恰好与轨道间没有相互作用力，故由重力提供向心力，根据圆周运动向心力公式即可得出最高点的速度；然后与M点的速度比较即可；根据重力做功求出小球重力势能的变化．
设小球通过轨道最高点时速度的大小为
，根据题意和圆周运动向心力公式得：
，解得：
，小球从M点到最高点的过程中，只有重力做负功，所以小球在最高点的速度小于小球在M点的速度．故A错误B正确；由几何关系可知，M与N之间的高度差
，所以小球从M点运动到N点过程中重力势能变化量为
，故C错误D正确．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】某实验小组用如下器材来测量电压表的内阻．
A．待测电压表（量程3V，内阻约几千欧）
B．电流表（量程0.6A，内阻约0.1Ω）
C．电池组（电动势约3V，内阻可忽略）
D．滑动变阻器R0
E．变阻箱R（0﹣9999Ω）
F．开关和导线若干
（1）图甲是某同学设计的电路，大家讨论后一致认为此电路不可行，你认为原因是____；
A．R0阻值较小
B．电流表存在内阻
C．电压表无法准确读数
D．电流表无法准确读数
（2）同学们改用图乙电路进行测量，设电阻箱的阻值R，电压表的示数为U，为了根据图像能求得电压表的内阻，应该作______图线（选“
”、填“U﹣R”、
）；
（3）请根据你选择的坐标轴和下表的数据，在图丙中标上合适的标度作出相应图线；
R/kΩ | 0.6 | 1.5 | 2 | 3 | 4 | 5 |
U/V | 2.5 | 2 | 1.8 | 1.5 | 1.3 | 1.13 |
| 1.67 | 0.67 | 0.5 | 0.33 | 0.25 | 0.20 |
| 0.40 | 0.50 | 0.56 | 0.67 | 0.78 | 0.88 |
（4）根据你所画出的图线，求出电源的电动势E=____V，电压表内阻Rv=______kΩ（保留两位有效数字）．
