题目内容
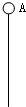 长为L的轻绳一端固定在O点,另一端栓一质量为m的小球,将小球拉到最高点A点,以v0=(
长为L的轻绳一端固定在O点,另一端栓一质量为m的小球,将小球拉到最高点A点,以v0=(| gL |
| 2 |
| 1 |
| 2 |
分析:求出小球在最高点做圆周运动的最小速度,若初速度大于最小速度,小球做圆周运动,若初速度小于最小速度,小球先做平抛运动,然后做圆周运动,在平抛运动转变为圆周运动的过程有能量损失.然后根据动能定理或机械能守恒求出最低点的速度,根据牛顿第二定律求出绳子的拉力.
解答:解:根据mg=m
,则在最高点做圆周运动的最小速度vmin=
.
v0<vmin,所以小球先做平抛运动,绳子拉直后做圆周运动.
设小球做平抛运动水平位移为x时,绳子拉直.
则平抛运动的时间t=
,平抛运动的竖直位移y=
gt2=
g
,
根据勾股定理,有x2+(L-y)2=L2,
将v0=
代入,
解得x=L.
知平抛运动的末位置正好与圆心在同一水平线上.
此时竖直分速度vy=
.
水平分速度不变,将水平分速度和竖直分速度沿半径方向和垂直于半径方向分解,
由于绳子绷紧,沿半径方向的速度立即消失,只剩下垂直于半径方向的速度,
此时的速度v=vy=
.
方法一:根据动能定理得,mgL=
mv′2-
mv2,解得v′2=4gL
根据牛顿第二定律得,F-mg=m
,解得F=5mg.
方法二:根据机械能守恒定律,
mv 2+mgL=
mv′2
解得v′2=4gL
根据牛顿第二定律得,F-mg=m
,解得F=5mg.
故小球经过最低点时绳子的拉力大小为5mg.
| vmin |
| L2 |
| gL |
v0<vmin,所以小球先做平抛运动,绳子拉直后做圆周运动.
设小球做平抛运动水平位移为x时,绳子拉直.
则平抛运动的时间t=
| x |
| v0 |
| 1 |
| 2 |
| 1 |
| 2 |
| x2 |
| v02 |
根据勾股定理,有x2+(L-y)2=L2,
将v0=
|
解得x=L.
知平抛运动的末位置正好与圆心在同一水平线上.
此时竖直分速度vy=
| 2gL |
水平分速度不变,将水平分速度和竖直分速度沿半径方向和垂直于半径方向分解,
由于绳子绷紧,沿半径方向的速度立即消失,只剩下垂直于半径方向的速度,
此时的速度v=vy=
| 2gL |
方法一:根据动能定理得,mgL=
| 1 |
| 2 |
| 1 |
| 2 |
根据牛顿第二定律得,F-mg=m
| v2 |
| L |
方法二:根据机械能守恒定律,
| 1 |
| 2 |
| 1 |
| 2 |
解得v′2=4gL
根据牛顿第二定律得,F-mg=m
| v2 |
| L |
故小球经过最低点时绳子的拉力大小为5mg.
点评:解决本题的关键确定小球的运动情况,知道若初速度大于最高点做圆周运动的最小速度,小球做圆周运动,若初速度小于最高点做圆周运动的最小速度,小球先做平抛运动,然后做圆周运动,在平抛运动转变为圆周运动的过程有能量损失.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 如图所示,一根长为L的轻绳一端固定在O′点,另一端系一质量m的小球,小球可视为质点.将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点时,轻绳刚好被拉断.O′点下方有一以O点为顶点的固定斜面,倾角θ=37°,斜面足够长,且OO′=2L,已知重力加速度为g,忽略空气阻力;求
如图所示,一根长为L的轻绳一端固定在O′点,另一端系一质量m的小球,小球可视为质点.将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点时,轻绳刚好被拉断.O′点下方有一以O点为顶点的固定斜面,倾角θ=37°,斜面足够长,且OO′=2L,已知重力加速度为g,忽略空气阻力;求 如图所示,长为L的轻绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,小球便可在水平面内做匀速圆周运动,这样就构成了一个圆锥摆,设轻绳与竖直方向的夹角为θ.下列说法正确的是( )
如图所示,长为L的轻绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,小球便可在水平面内做匀速圆周运动,这样就构成了一个圆锥摆,设轻绳与竖直方向的夹角为θ.下列说法正确的是( )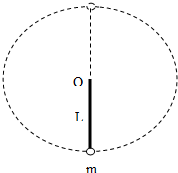 如图所示,长为L的轻绳一端固定在O点,另一端拴有一个质量为m的小球.现在使小球在竖直平面内做圆周运动,并能通过最高点,则下列说法正确的是( )
如图所示,长为L的轻绳一端固定在O点,另一端拴有一个质量为m的小球.现在使小球在竖直平面内做圆周运动,并能通过最高点,则下列说法正确的是( )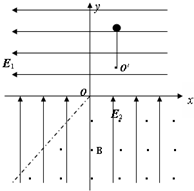 如图所示,在x轴上方有水平向左的匀强电场E1,在x轴下方有竖直向上的匀强电场E2,且
如图所示,在x轴上方有水平向左的匀强电场E1,在x轴下方有竖直向上的匀强电场E2,且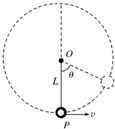 如图所示,长为L的轻绳一端固定在O点,另一端系一小球(可视为质点),小球在竖直平面内沿逆时针方向做圆周运动.已知小球运动过程中轻绳拉力大小FT和竖直方向OP的夹角θ的关系为:FT=b+bcosθ,b为已知的常数,当地重力加速度为g,不计空气阻力,求小球的质量.
如图所示,长为L的轻绳一端固定在O点,另一端系一小球(可视为质点),小球在竖直平面内沿逆时针方向做圆周运动.已知小球运动过程中轻绳拉力大小FT和竖直方向OP的夹角θ的关系为:FT=b+bcosθ,b为已知的常数,当地重力加速度为g,不计空气阻力,求小球的质量.