题目内容
(10分)如图所示,滑板运动员从倾角为53°的斜坡顶端滑下,滑下的过程中他突然发现在斜面底端有一个高h=1.4m、宽L=1.2m的长方体障碍物,为了不触及这个障碍物,他必须距水平地面高度H=3.2m的A点沿水平方向跳起离开斜面。已知运动员的滑板与斜面间的动摩擦因数μ=0.1,忽略空气阻力,重力加速度g取10m/s2。(已知sin53°=0.8,cos53°=0.6)求:
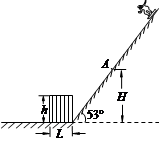
(1)运动员在斜面上滑行的加速度的大小;
(2)若运动员不触及障碍物,他从斜面上起跳后到落至水平面的过程所经历的时间;
(3)运动员为了不触及障碍物,他从A点沿水平方向起跳的最小速度

(1)运动员在斜面上滑行的加速度的大小;
(2)若运动员不触及障碍物,他从斜面上起跳后到落至水平面的过程所经历的时间;
(3)运动员为了不触及障碍物,他从A点沿水平方向起跳的最小速度
(1)7.4m/s2(2)0.8s(3)6.0m/s
试题分析:解:(1)设运动员连同滑板的质量为m,运动员在斜面上滑行的过程中,根据牛顿第二定律
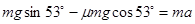
解得运动员在斜面上滑行的加速度
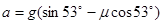 =7.4m/s2
=7.4m/s2(2)从运动员斜面上起跳后沿竖直方向做自由落体运动,根据自由落体公式
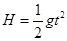
解得
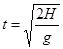 =0.8s
=0.8s (3)为了不触及障碍物,运动员以速度v沿水平方向起跳后竖直下落高度为H-h时,他沿水平方向的运动的距离为Hcot53°+L,设他在这段时间内运动的时间为t′,则

Hcot53°+L=vt′
解得v=6.0m/s
点评:此类题型考察了物理题型中重要的模型:平抛运动。结合牛顿运动定律分析物体运动的加速度,通过分析平抛找出等式关系。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
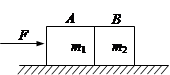
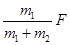


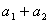
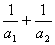
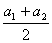
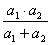
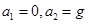
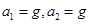
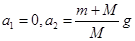
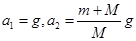

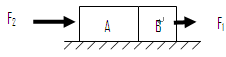
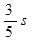 B.
B.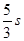 C.2s D.3s
C.2s D.3s