题目内容
(15分)如图所示,两根足够长、电阻不计的平行光滑金属导轨处于磁感应强度大小为B=0.5T的匀强磁场中,导轨平面与水平面成θ=30°角,下端连接“2.5V,0.5W”的小电珠,磁场方向与导轨平面垂直,质量为m=0.02kg、电阻不计的光滑金属棒与导轨垂直并保持良好接触,金属棒由静止开始释放,下滑速度达到稳定时,小电珠正常发光,取g=10m/s2,求:
⑴金属棒沿轨道下滑时对轨道的压力大小;
⑵金属导轨的宽度;
⑶金属棒稳定下滑时的速度大小。
⑴N′=0.173N;⑵d=1m;⑶v=5m/s
解析试题分析:⑴金属棒沿轨道下滑时,对金属棒,受重力mg、导轨的支持力N和磁场的安培力F作用,在垂直于导轨方向上有:N-mgcosθ=0 ①
根据牛顿第三定律可知,金属棒对轨道的压力为:N′=N ②
由①②式联立解得:N′=mgcosθ=0.02×10× N=
N= N=0.173N
N=0.173N
⑵当金属棒匀速下滑时,其下滑速度达到稳定,因此在沿导轨向下方向上,有:mgsinθ-F=0 ③
设稳定时回路中的电流为I,金属导轨的宽度为d,根据安培力大小计算公式有:F=IdB ④
根据功率、电压与电流的关系,有:I=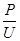 ⑤
⑤
由③④⑤式联立解得:d=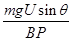 =
=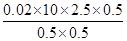 m=1m ⑥
m=1m ⑥
⑶由于电路中其它部分电阻不计,因此,金属棒切割磁感线产生的感应电动势E=U ⑦
根据法拉第电磁感应定律可知:E=Bdv ⑧
由⑥⑦⑧式联立解得金属棒稳定下滑时的速度大小为:v=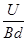 =
=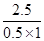 m/s=5m/s
m/s=5m/s
考点:本题主要考查了共点力平衡条件、牛顿运动定律、法拉第电磁感应定律的应用及电功率的计算问题,属于中档题。

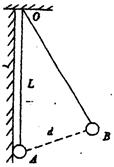
一块木板可绕过O点的光滑水平轴在竖直平面内转动,木板上放有一木块,木板右端受到始终与木板垂直的力F,从图中位置A缓慢转到位置B,木块相对木板不发生滑动。则在此过程中,力F和F的力矩MF大小的变化情况是( )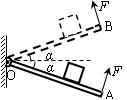
| A.F始终保持不变,MF先变小后变大 |
| B.F始终保持不变,MF先变大后变小 |
| C.F先变大后变小,MF先变小后变大 |
| D.F先变大后变小,MF先变大后变小 |
下列关于力和运动的关系的说法中,正确的是( )
| A.没有外力作用时,物体不会运动,这是牛顿第一定律的体现 |
| B.物体受合外力越大,运动得越快,这是符合牛顿第二定律的 |
| C.直线运动的物体所受合外力突变时,速度的大小和方向也会发生突变 |
| D.物体所受合外力最大时,速度可能为零 |
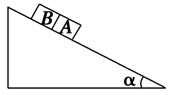
 的A、B物块紧靠着在倾角为
的A、B物块紧靠着在倾角为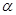 粗糙斜面上一起加速下滑,斜面与A之间动摩擦因数为
粗糙斜面上一起加速下滑,斜面与A之间动摩擦因数为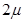 ,与B之间动摩擦因数为
,与B之间动摩擦因数为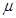 ,已知重力加速度为
,已知重力加速度为 。
。
 =37°,两导轨之间距离为L=0.2m,导轨上端m、n之间通过导线连接,有理想边界的匀强磁场垂直于导轨平面向上,虚线ef为磁场边界,磁感应强度为B=2.0T。一质量为m=0.05kg的光滑金属棒ab从距离磁场边界0.75m处由静止释放,金属棒两轨道间的电阻r=0.4
=37°,两导轨之间距离为L=0.2m,导轨上端m、n之间通过导线连接,有理想边界的匀强磁场垂直于导轨平面向上,虚线ef为磁场边界,磁感应强度为B=2.0T。一质量为m=0.05kg的光滑金属棒ab从距离磁场边界0.75m处由静止释放,金属棒两轨道间的电阻r=0.4 其余部分的电阻忽略不计,ab、ef均垂直导轨。(g=10m/s2,sin37°=0.6,cos37°=0.8),求:
其余部分的电阻忽略不计,ab、ef均垂直导轨。(g=10m/s2,sin37°=0.6,cos37°=0.8),求: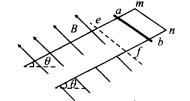
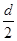 ,求q1/q2;
,求q1/q2;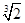 d,求m1/m2.
d,求m1/m2.