题目内容
(14分)如图所示,两足够长的平行光滑金属导轨倾斜放置,与水平面间的夹角为 =37°,两导轨之间距离为L=0.2m,导轨上端m、n之间通过导线连接,有理想边界的匀强磁场垂直于导轨平面向上,虚线ef为磁场边界,磁感应强度为B=2.0T。一质量为m=0.05kg的光滑金属棒ab从距离磁场边界0.75m处由静止释放,金属棒两轨道间的电阻r=0.4
=37°,两导轨之间距离为L=0.2m,导轨上端m、n之间通过导线连接,有理想边界的匀强磁场垂直于导轨平面向上,虚线ef为磁场边界,磁感应强度为B=2.0T。一质量为m=0.05kg的光滑金属棒ab从距离磁场边界0.75m处由静止释放,金属棒两轨道间的电阻r=0.4 其余部分的电阻忽略不计,ab、ef均垂直导轨。(g=10m/s2,sin37°=0.6,cos37°=0.8),求:
其余部分的电阻忽略不计,ab、ef均垂直导轨。(g=10m/s2,sin37°=0.6,cos37°=0.8),求: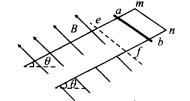
(1)ab棒最终在磁场中匀速运动时的速度;
(2)ab棒运动过程中的最大加速度。
(1)0.75m/s (2)18m/s2,方向沿斜面向上
解析试题分析:(1)当ab棒在磁场中匀速运动时,分析ab棒的受力,根据受力平衡得: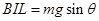
又有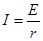 和
和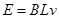 ,联立以上关系可得v=0.75m/s
,联立以上关系可得v=0.75m/s
(2)在ab棒进入磁场前分析得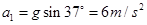 ,方向沿轨道向下
,方向沿轨道向下
进入磁场时的速度设为v2,由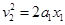
由于位移等于x1=0.75m,则v2=3m/s
刚进入磁场时,对ab棒的分析受力得: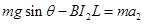 ,
,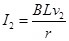
解得a2=-18m/s2,方向沿导轨向上
进入磁场以后,ab棒做加速度逐渐减小的减速运动,最终匀速运动,
所以,ab棒运动中的最大加速度为18m/s2,方向沿斜面向上。
考点:本题考查物体的平衡条件,运动学关系和牛顿第二定律。

练习册系列答案
相关题目
(多选)下列说法中正确的是( )
| A.物体抵抗运动状态变化的性质是惯性 |
| B.牛顿第一定律、牛顿第二定律都可以通过实验来验证 |
| C.单位m、kg、s是一组属于国际单位制的基本单位 |
D.根据速度定义式v=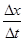 ,当Δt→0时, ,当Δt→0时,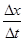 就可以表示物体在t时刻的瞬时速度,该定义运用了极限思维法 就可以表示物体在t时刻的瞬时速度,该定义运用了极限思维法 |
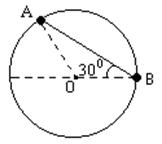
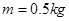 的小物块,在水平力
的小物块,在水平力 的作用下静止于P点。已知PO与水平方向的夹角
的作用下静止于P点。已知PO与水平方向的夹角 ,圆弧轨道的半径
,圆弧轨道的半径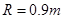 ,圆弧轨道光滑,物块与水平轨道BC之间的滑动摩擦因数
,圆弧轨道光滑,物块与水平轨道BC之间的滑动摩擦因数 。重力加速度
。重力加速度 .求:
.求:
 ;
; .
. ,其活塞为梯形,它的一个面与气缸成
,其活塞为梯形,它的一个面与气缸成 角,活塞与器壁间的摩擦忽略不计,现用一水平力
角,活塞与器壁间的摩擦忽略不计,现用一水平力 推活塞,汽缸不动,此时大气压强为
推活塞,汽缸不动,此时大气压强为 ,求气缸内气体的压强
,求气缸内气体的压强 .
.
 的“U”型金属框架下端连接一阻值为
的“U”型金属框架下端连接一阻值为 的电阻,相互平行的金属杆MN、PQ间距为
的电阻,相互平行的金属杆MN、PQ间距为 ,与金属杆垂直的虚线
,与金属杆垂直的虚线 、
、 区域内有垂直框架平面向上的匀强磁场,磁感应强度大小为
区域内有垂直框架平面向上的匀强磁场,磁感应强度大小为 ,
, ,一长为
,一长为 、电阻为
、电阻为 (金属框架摩擦及电阻不计).求:
(金属框架摩擦及电阻不计).求:
 ;
; ;
;
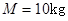 ,长为
,长为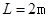 的木板放在水平地面上,已知木板与地面间的动摩擦因数为
的木板放在水平地面上,已知木板与地面间的动摩擦因数为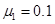 ,在此木板的右端上还有一质量为
,在此木板的右端上还有一质量为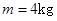 的小物块,且视小物块为质点,木板厚度不计. 今对木板突然施加一个
的小物块,且视小物块为质点,木板厚度不计. 今对木板突然施加一个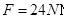 的水平向右的拉力,
的水平向右的拉力,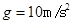 .
.
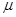 、小物块与地面间的动摩擦因数为
、小物块与地面间的动摩擦因数为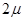 ,小物块相对木板滑动且对地面的总位移
,小物块相对木板滑动且对地面的总位移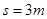 ,求
,求