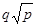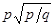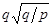题目内容
两颗人造卫星A、B绕地球做匀速圆周运动，它们的周期之比TA∶TB=1∶8，则其轨道半径之比是 运动速率之比是
1:4 2:1
分析：人造卫星绕地球做圆周运动受到的万有引力提供向心力，分别用周期、速率来表示向心力，化简公式即可求解结果．
解答：解：人造卫星绕地球做圆周运动受到的万有引力提供向心力，对A卫星有：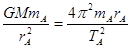
，
对B卫星有：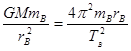
，化简得：
= 
；
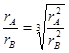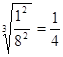用速度表示向心力，对A卫星有：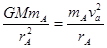
， 对B卫星有：
，
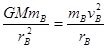化简得：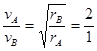
，
故答案为：1：4，2：1．
点评：对于卫星问题一定掌握：万有引力提供向心力，可以用卫星的速度、周期、角速度来分别表示向心力，从而求出结果．
解答：解：人造卫星绕地球做圆周运动受到的万有引力提供向心力，对A卫星有：
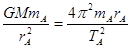，对B卫星有：
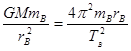，化简得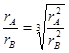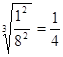：= ；用速度表示向心力，对A卫星有：
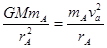， 对B卫星有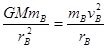：，化简得：
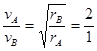，故答案为：1：4，2：1．
点评：对于卫星问题一定掌握：万有引力提供向心力，可以用卫星的速度、周期、角速度来分别表示向心力，从而求出结果．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
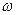0,某一时刻该卫星通过赤道上某建筑物的正上方, 再经过多少时间它又一次出现在该建筑物正上方？
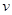环绕火星表面飞行。若认为地球和火星都是质量分布均匀的球体，已知地球和火星的半径之比为
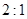，密度之比为
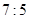，则v约等于：
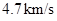
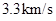
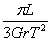
的近地圆轨道，然后在地面的指令下经过一系列的变轨后最终被月球捕获，经两次制动后在距离月球表面为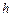
的轨道上绕月球做匀速圆周运动． 已知地球质量为
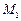，半径为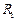
，月球质量为
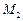，半径为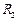
． 求：“嫦娥二号”绕月球运动时的周期
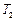（最终结果用题目中的物理量来表示）．
