题目内容
10.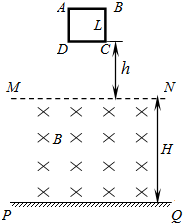 如图所示,正方形线框ABCD在有界匀强磁场边界MN上方某处处于静止状态,线框平面在纸面里,CD边平行于MN,CD到MN的距离为h,线框的质量为m,电阻为R,边长为L,线框共有N匝,匀强磁场磁感应强度大小为B,方向垂直于纸面向里,磁场两边界MN、PQ水平,间距为H,H>L,由静止释放线框,线框在下落过程中始终保持竖直且CD边始终保持水平,CD边刚进入磁场时线框的加速度为零,AB边刚要出磁场时加速度也为零,则 ( )
如图所示,正方形线框ABCD在有界匀强磁场边界MN上方某处处于静止状态,线框平面在纸面里,CD边平行于MN,CD到MN的距离为h,线框的质量为m,电阻为R,边长为L,线框共有N匝,匀强磁场磁感应强度大小为B,方向垂直于纸面向里,磁场两边界MN、PQ水平,间距为H,H>L,由静止释放线框,线框在下落过程中始终保持竖直且CD边始终保持水平,CD边刚进入磁场时线框的加速度为零,AB边刚要出磁场时加速度也为零,则 ( )| A. | CD离MN的距离为$\frac{{m}^{2}g{R}^{2}}{2{N}^{2}{B}^{4}{L}^{4}}$ | |
| B. | 线框进磁场的过程中通过线框某一导线横截面的电荷量为$\frac{NB{L}^{2}}{R}$ | |
| C. | 线框CD边刚出磁场时的速度大小为$\sqrt{\frac{{m}^{2}{g}^{2}{R}^{2}}{{N}^{4}{B}^{4}{L}^{4}}+gH}$ | |
| D. | 线框进磁场产生的焦耳热与出磁场产生的焦耳热之比为$\frac{L}{H}$ |
分析 明确物理过程,根据共点力的平衡条件及功能关系进行分析,则可求得速度及产生的热量;根据法拉第电磁感应定律可求得产生的电量.
解答 解:A、CD边进入磁场时,加速度为零,则有安培力和重力大小相等,即mg=NBIL=N2$\frac{{B}^{2}{L}^{2}v}{R}$;
由机械能守恒定律可知mgh=$\frac{1}{2}$mv2;联立解得:h=$\frac{{m}^{2}g{R}^{2}}{2{N}^{4}{B}^{4}{L}^{4}}$;故A错误;
B、产生的电量q=$\overline{I}$t=$\frac{NBS}{R}$=$\frac{NB{L}^{2}}{R}$;故B正确;
C、由题意可知,线框ABCD进入磁场的过程速度不变,从AB边刚进入磁场到CD边刚要出磁场的过程,由机械能守恒定律可知:
$\frac{1}{2}$mv2+mg(H-L)=$\frac{1}{2}$mv12,
所以CD边刚出磁场时的速度大小为$\sqrt{\frac{{m}^{2}{g}^{2}{R}^{2}}{{N}^{4}{B}^{4}{L}^{4}}+2g(H-L)}$,
故C错误;
D、由题意可知,线框ABCD进入磁场的过程中重力势能等于焦耳热,则Q进=mgL,
由于CD刚进入磁场时和AB边刚要离开磁场时的速度相等,则线框ABCD从AB边刚进入磁场到AB边刚离开磁场的过程,由能量守恒定律可知:
$\frac{1}{2}$mv2+mgH=$\frac{1}{2}$mv2+Q出,
所以Q出=mgH,
则$\frac{{Q}_{进}}{{Q}_{出}}$=$\frac{L}{H}$,
故D正确.
故选:BD.
点评 本题考查导体切割磁感线中的受力及能量关系,要注意明确物理过程的正确选择,同时要注意掌握求电量的基本方法.

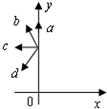 一匀强磁场,磁场方向垂直于xOy平面,在xOy平面上,磁场分布在图中第一象限内.一个质量为m、电荷量为q的带电粒子,由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响.粒子经过P点时的速度方向可能是图中箭头表示的( )
一匀强磁场,磁场方向垂直于xOy平面,在xOy平面上,磁场分布在图中第一象限内.一个质量为m、电荷量为q的带电粒子,由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响.粒子经过P点时的速度方向可能是图中箭头表示的( )| A. | 只有箭头a、b是可能的 | B. | 只有箭头b、c是可能的 | ||
| C. | 只有箭头c是可能的 | D. | 箭头a、b、c、d都是可能的 |
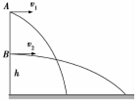 如图所示,A、B两个小球在同一竖直线上,离地高度分别为h和2h,将两球水平抛出后,两球落地时的水平位移之比为1:2,则下列说法正确的是 ( )
如图所示,A、B两个小球在同一竖直线上,离地高度分别为h和2h,将两球水平抛出后,两球落地时的水平位移之比为1:2,则下列说法正确的是 ( )| A. | A、B两球的初速度之比为1:4 | |
| B. | A、B两球的初速度之比为1:2 | |
| C. | 若两球同时抛出,则落地时间差为$\sqrt{\frac{2h}{g}}$ | |
| D. | 若两球同时落地,则两球抛出的时间差为($\sqrt{2}-1$)$\sqrt{\frac{2h}{g}}$ |
| A. | v | B. | 2v | C. | 3v | D. | 4v |
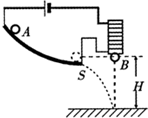 如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开轻质接触式开关S,被电磁铁吸住的小球B同时自由下落.多次改变整个装置的高度做同样的实验,会发现位于同一高度的A、B两球总是同时落地的现象;该实验现象说明了A球的离开轨道后,C.
如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开轻质接触式开关S,被电磁铁吸住的小球B同时自由下落.多次改变整个装置的高度做同样的实验,会发现位于同一高度的A、B两球总是同时落地的现象;该实验现象说明了A球的离开轨道后,C. 如图所示,一导热性能良好、内壁光滑的气缸开口向右放置,在距气缸底部L=24cm处有一与气缸固定连接的卡环,活塞与气缸底部之间封闭了一定质量的气体.活塞截面积为500cm2,大气压强p0=1.0×105Pa,当大气温度为T0=300K时,活塞与气缸底部之间的距离 L0=16cm,不计活塞的厚度.现对气缸加热,使活塞缓慢向右移,求:
如图所示,一导热性能良好、内壁光滑的气缸开口向右放置,在距气缸底部L=24cm处有一与气缸固定连接的卡环,活塞与气缸底部之间封闭了一定质量的气体.活塞截面积为500cm2,大气压强p0=1.0×105Pa,当大气温度为T0=300K时,活塞与气缸底部之间的距离 L0=16cm,不计活塞的厚度.现对气缸加热,使活塞缓慢向右移,求: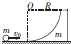 如图所示,光滑水平面上有带有$\frac{1}{4}$光滑圆弧轨道的滑块,其质量为m,另一质量也为m的小球以速度v0沿水平面滑上轨道,若小球不能从轨道上端飞出,系统在相互作用的过程中没有机械能的损失,重力加速度为g,求小球上升的最大高度.
如图所示,光滑水平面上有带有$\frac{1}{4}$光滑圆弧轨道的滑块,其质量为m,另一质量也为m的小球以速度v0沿水平面滑上轨道,若小球不能从轨道上端飞出,系统在相互作用的过程中没有机械能的损失,重力加速度为g,求小球上升的最大高度. 如图所示,用网兜把一蓝球挂在竖直光滑墙壁上的A点,蓝球与墙壁的接触点为B.已知蓝球的质量是600g,直径是24.6cm,AB间的距离是16.4cm,AC为悬绳,不计网兜和悬绳的质量(cos37°=0.8,sin37°=0.6 ).求:
如图所示,用网兜把一蓝球挂在竖直光滑墙壁上的A点,蓝球与墙壁的接触点为B.已知蓝球的质量是600g,直径是24.6cm,AB间的距离是16.4cm,AC为悬绳,不计网兜和悬绳的质量(cos37°=0.8,sin37°=0.6 ).求: