Question

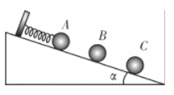
【题目】如图所示，质量为mA=2kg的铁块叠放在质量为mB=0.5kg的木板上面，一起静止在足够长的斜面上，现通过斜面顶端的定滑轮，用平行斜面的细线拉着A匀加速运动。已知铁块与木板之间的动摩擦因数，木板长l=1m，斜面倾角，图乙是物体B在斜面上运动的速度与时间图象。g取10m/s2，sin37°=0.6，cos37°=0.8。求：

（1）细线拉力F的大小

（2）木板在斜面上的总位移

Answer 1

【答案】（1） 28N （2）

【解析】

（1）由图乙可知B先做加速运动，A离开后做减速运动，由图乙知B加速阶段的加速度为

a1=2m/s2

设A的加速度为a，它在B上滑动过程中运动的位移为

B加速过程的位移为

由几何关系可知

xA-xB=l

代入，t=1s，l=1m解得

a=4m/s2

分析A加速过程中的受力情况如图一：

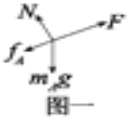
由牛顿第二定律得：

而

⑤

联立得

F = 28N

（2）分析B物体加速阶段的受力情况如图二：

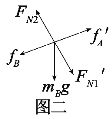
由牛顿第二定律可得：

fA′-fB-mBgsinα=mBa1

设B与斜面的动摩擦因数为μ2，有

联立解得

μ2=0.2

由牛顿第二定律可知B减速的加速度

=7.6m/s2

由图乙可知B加速的位移

x1=×2×1m=1m

根据匀变速直线运动规律减速的性质

m

所以木板的总位移

m