题目内容
8.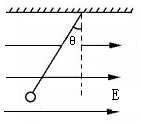 如图所示,一质量m=12g,带电荷量q=3.0×10-6C 的小球,用绝缘细线悬挂在水平向右的匀强电场中,静止时悬线向左与竖直方向成θ=37°角.
如图所示,一质量m=12g,带电荷量q=3.0×10-6C 的小球,用绝缘细线悬挂在水平向右的匀强电场中,静止时悬线向左与竖直方向成θ=37°角.(1)判断小球带何种电荷;
(2)求电场强度的大小;
(3)若将细线剪断,经过1s小球的速度是多大?(还在电场中,小球未落地)
分析 (1)小球处于静止状态,分析受力,作出力图,根据电场力与场强方向的关系判断电性.
(2)根据平衡条件和电场力公式求解场强.
(3)将细线突然剪断小球将沿细线方向做匀加速直线运动,根据牛顿第二定律和速度公式结合求解v.
解答 解:(1)小球受力如图,由于电场力F与场强方向相反,说明小球带负电.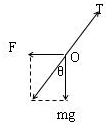
(2)小球的电场力为:F=qE
由平衡条件得:F=mgtanθ
解得电场强度为:E=$\frac{mgtanθ}{q}$=3×104 N/C
(3)剪断细线后小球做初速度为0的匀加速直线运动,经过1s时小球的速度为v.
小球所受合外力为:F合=$\frac{mg}{cosθ}$
由牛顿第二定律有:F合=ma
又运动学公式为:v=at
解得小球的速度为:v=12.5m/s
速度方向为与竖直方向夹角为37°斜向下.
答:(1)小球带负电荷.
(2)电场强度为3×104 N/C.
(3)若在某时刻将细线突然剪断,经过1s时小球的速度为12.5m/s.
点评 对于涉及物体运动的问题,两大分析:受力情况分析和运动情况分析是基础,要培养这方面的基本功.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
18.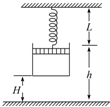 如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
 如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )| A. | 活塞高度h | B. | 汽缸底距地面高度H | ||
| C. | 气体压强p | D. | 弹簧长度L |
16.某导体中的电流随其两端电压的变化如图所示,下列说法正确的是( )
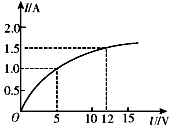

| A. | 加5 V电压时,导体的电阻约是5Ω | |
| B. | 加12 V电压时,导体的电阻约是1.4Ω | |
| C. | 由图可知随着电压的增大,导体的电阻不断减小 | |
| D. | 由图可知随着电压的减小,导体的电阻不断减小 |
13.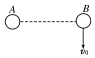 如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,B球将( )
如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,B球将( )
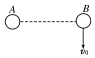 如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,B球将( )
如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,B球将( )| A. | 若A、B为异种电荷,B球可能做圆周运动 | |
| B. | 若A、B为异种电荷,B球一定做加速度、速度均变小的曲线运动 | |
| C. | 若A、B为同种电荷,B球一定做远离A的变加速曲线运动 | |
| D. | 若A、B为同种电荷,B球的动能一定会减小 |
18.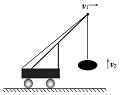 如图所示,吊车沿水平地面以速度v1匀速行驶,同时以大小恒定的速度v2收拢绳索提升物体时,下列表述正确的是( )
如图所示,吊车沿水平地面以速度v1匀速行驶,同时以大小恒定的速度v2收拢绳索提升物体时,下列表述正确的是( )
 如图所示,吊车沿水平地面以速度v1匀速行驶,同时以大小恒定的速度v2收拢绳索提升物体时,下列表述正确的是( )
如图所示,吊车沿水平地面以速度v1匀速行驶,同时以大小恒定的速度v2收拢绳索提升物体时,下列表述正确的是( )| A. | 物体的实际运动速度为v1+v2 | B. | 物体相对地面做曲线运动 | ||
| C. | 绳索始终保持竖直状态 | D. | 物体实际运动方向始终竖直向上 |
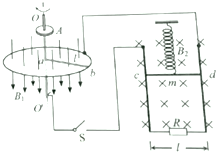 为了探究电动机转速与弹簧伸长量之间的关系,小明设计了如图所示的装置.半径为l的圆形金属导轨固定在水平面上,一根长也为l、电阻为R的金属棒ab一端与导轨接触良好,另一端固定在圆心处的导电转轴oo’上,由电动机A带动旋转.在金属导轨区域内存在垂直于导轨平面,大小为B1、方向竖直向下的匀强磁场.另有一质量为m、电阻为R的金属棒cd用轻质弹簧悬挂在竖直平面内,并与固定在竖直平面内的“U”型导轨保持良好接触,导轨间距为l,底部接阻值也为R的电阻,处于大小为B2、方向垂直导轨平面向里的匀强磁场中,从圆形金属导轨引出导线和通过电刷从转轴引出导线经开关S与“U”型导轨连接.当开关S断开,棒cd静止时,弹簧伸长量为x0;当开关S闭合,电动机以某一速度匀速转动,棒cd再次静止,弹簧伸长量变为x(不超过弹性限度).不计其余电阻和摩擦等阻力,求此时
为了探究电动机转速与弹簧伸长量之间的关系,小明设计了如图所示的装置.半径为l的圆形金属导轨固定在水平面上,一根长也为l、电阻为R的金属棒ab一端与导轨接触良好,另一端固定在圆心处的导电转轴oo’上,由电动机A带动旋转.在金属导轨区域内存在垂直于导轨平面,大小为B1、方向竖直向下的匀强磁场.另有一质量为m、电阻为R的金属棒cd用轻质弹簧悬挂在竖直平面内,并与固定在竖直平面内的“U”型导轨保持良好接触,导轨间距为l,底部接阻值也为R的电阻,处于大小为B2、方向垂直导轨平面向里的匀强磁场中,从圆形金属导轨引出导线和通过电刷从转轴引出导线经开关S与“U”型导轨连接.当开关S断开,棒cd静止时,弹簧伸长量为x0;当开关S闭合,电动机以某一速度匀速转动,棒cd再次静止,弹簧伸长量变为x(不超过弹性限度).不计其余电阻和摩擦等阻力,求此时
