题目内容
19.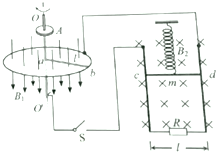 为了探究电动机转速与弹簧伸长量之间的关系,小明设计了如图所示的装置.半径为l的圆形金属导轨固定在水平面上,一根长也为l、电阻为R的金属棒ab一端与导轨接触良好,另一端固定在圆心处的导电转轴oo’上,由电动机A带动旋转.在金属导轨区域内存在垂直于导轨平面,大小为B1、方向竖直向下的匀强磁场.另有一质量为m、电阻为R的金属棒cd用轻质弹簧悬挂在竖直平面内,并与固定在竖直平面内的“U”型导轨保持良好接触,导轨间距为l,底部接阻值也为R的电阻,处于大小为B2、方向垂直导轨平面向里的匀强磁场中,从圆形金属导轨引出导线和通过电刷从转轴引出导线经开关S与“U”型导轨连接.当开关S断开,棒cd静止时,弹簧伸长量为x0;当开关S闭合,电动机以某一速度匀速转动,棒cd再次静止,弹簧伸长量变为x(不超过弹性限度).不计其余电阻和摩擦等阻力,求此时
为了探究电动机转速与弹簧伸长量之间的关系,小明设计了如图所示的装置.半径为l的圆形金属导轨固定在水平面上,一根长也为l、电阻为R的金属棒ab一端与导轨接触良好,另一端固定在圆心处的导电转轴oo’上,由电动机A带动旋转.在金属导轨区域内存在垂直于导轨平面,大小为B1、方向竖直向下的匀强磁场.另有一质量为m、电阻为R的金属棒cd用轻质弹簧悬挂在竖直平面内,并与固定在竖直平面内的“U”型导轨保持良好接触,导轨间距为l,底部接阻值也为R的电阻,处于大小为B2、方向垂直导轨平面向里的匀强磁场中,从圆形金属导轨引出导线和通过电刷从转轴引出导线经开关S与“U”型导轨连接.当开关S断开,棒cd静止时,弹簧伸长量为x0;当开关S闭合,电动机以某一速度匀速转动,棒cd再次静止,弹簧伸长量变为x(不超过弹性限度).不计其余电阻和摩擦等阻力,求此时(1)通过棒cd的电流Icd;
(2)电动机对该装置的输出功率P;
(3)电动机转动角速度ω与弹簧伸长量x之间的函数关系.
分析 (1)S断开和闭合时,根据平衡条件列式,即可求出棒cd的电流;
(2)电动机对该装置的输出功率等于回路电阻上消耗的热功率;
(3)根据法拉第电磁感应定律和欧姆定律求出回路总电流,联立(2),即可得出电动机转动角速度ω与弹簧伸长量x之间的函数关系
解答 解:(1)S断开,cd棒静止有:
$mg=k{x}_{0}^{\;}$
S闭合,cd棒静止时受到的安培力为:
$F={I}_{cd}^{\;}{B}_{2}^{\;}l$
cd棒静止有:
$mg+{I}_{cd}^{\;}{B}_{2}^{\;}l=kx$
得:${I}_{cd}^{\;}=\frac{mg(x-{x}_{0}^{\;})}{{B}_{2}^{\;}l{x}_{0}^{\;}}$
(2)回路总电阻为:${R}_{总}^{\;}=R+\frac{1}{2}R=\frac{3}{2}R$
总电流为:$I=\frac{2mg(x-{x}_{0}^{\;})}{{B}_{2}^{\;}l{x}_{0}^{\;}}$
由能量守恒得:$P={I}_{\;}^{2}{R}_{总}^{\;}=\frac{6{m}_{\;}^{2}{g}_{\;}^{2}R(x-{x}_{0}^{\;})_{\;}^{2}}{{B}_{2}^{2}{l}_{\;}^{2}{x}_{0}^{2}}$
(3)由法拉第电磁感应定律:
$E=\frac{△Φ}{△t}=\frac{1}{2}{B}_{1}^{\;}ω{l}_{\;}^{2}$
回路总电流为:$I=\frac{{B}_{1}^{\;}ω{l}_{\;}^{2}}{3R}$
解得:$ω=\frac{6mgR(x-{x}_{0}^{\;})}{{B}_{1}^{\;}{B}_{2}^{\;}{l}_{\;}^{3}{x}_{0}^{\;}}$
答:(1)通过棒cd的电流$\frac{mg(x-{x}_{0}^{\;})}{{B}_{2}^{\;}l{x}_{0}^{\;}}$;
(2)电动机对该装置的输出功率P为$\frac{6{m}_{\;}^{2}{g}_{\;}^{2}R(x-{x}_{0}^{\;})_{\;}^{2}}{{B}_{2}^{2}{l}_{\;}^{2}{x}_{0}^{2}}$;
(3)电动机转动角速度ω与弹簧伸长量x之间的函数关系$ω=\frac{6mgR(x-{x}_{0}^{\;})}{{B}_{1}^{\;}{B}_{2}^{\;}{l}_{\;}^{3}{x}_{0}^{\;}}$.
点评 本题考查了电磁感应与电学、力学知识的综合,关键是掌握转动感应电动势公式$E=\frac{1}{2}B{R}_{\;}^{2}ω$,注意理清电路结构,切割磁感线的导体棒相当于电源.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
| A. | 往复运动 | B. | 加速度大小始终不变 | ||
| C. | 3s末速度为零 | D. | 6s末位移为零 |
| A. | $\frac{t}{2}$时物体距地面高度为$\frac{H}{2}$ | B. | $\frac{t}{2}$时物体距地面高度为$\frac{3H}{4}$ | ||
| C. | 物体下落$\frac{H}{2}$时速度为$\frac{\sqrt{2}v}{2}$ | D. | 物体下落$\frac{H}{2}$时速度为$\frac{v}{2}$ |
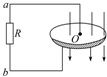 如图所示,金属圆盘可绕O轴转动,电阻R用电刷接于圆盘中心和边缘之间.当圆盘做顺时针方向的转动时(从上向下看),通过R的电流方向是b→a.
如图所示,金属圆盘可绕O轴转动,电阻R用电刷接于圆盘中心和边缘之间.当圆盘做顺时针方向的转动时(从上向下看),通过R的电流方向是b→a. 如图所示,在相互垂直的匀强电场和匀强磁场中,水平放置一足够长的绝缘直棒,棒上套着一个带正电的小球,电场强度为E,方向水平向右;磁感应强度为B,方向垂直纸面向里.小球质量为m,带电荷量为+q,小球沿水平棒滑动时摩擦因数为μ.小球刚开始向右滑动后,求:
如图所示,在相互垂直的匀强电场和匀强磁场中,水平放置一足够长的绝缘直棒,棒上套着一个带正电的小球,电场强度为E,方向水平向右;磁感应强度为B,方向垂直纸面向里.小球质量为m,带电荷量为+q,小球沿水平棒滑动时摩擦因数为μ.小球刚开始向右滑动后,求: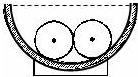 如图所示,两个质量均为0.4kg的光滑球,其半径均为r=3cm,将其放置在光滑半球形碗底,半球形碗口各处处于同一水平面上.两球最终在半径R=8cm的光滑半球形碗底稳定后处于静止状态,求两球之间相互作用力的大小(取g=10m/s2,sin 37°=0.6,cos 37°=0.8)
如图所示,两个质量均为0.4kg的光滑球,其半径均为r=3cm,将其放置在光滑半球形碗底,半球形碗口各处处于同一水平面上.两球最终在半径R=8cm的光滑半球形碗底稳定后处于静止状态,求两球之间相互作用力的大小(取g=10m/s2,sin 37°=0.6,cos 37°=0.8)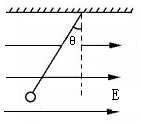 如图所示,一质量m=12g,带电荷量q=3.0×10-6C 的小球,用绝缘细线悬挂在水平向右的匀强电场中,静止时悬线向左与竖直方向成θ=37°角.
如图所示,一质量m=12g,带电荷量q=3.0×10-6C 的小球,用绝缘细线悬挂在水平向右的匀强电场中,静止时悬线向左与竖直方向成θ=37°角.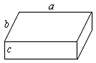 如图所示,一段长为a,宽为b,高为c(a>b>c)的导体,将其中的两个对立面接入电路中时,最大的电阻为R,则最小的电阻为$\frac{{c}^{2}R}{{a}^{2}}$.
如图所示,一段长为a,宽为b,高为c(a>b>c)的导体,将其中的两个对立面接入电路中时,最大的电阻为R,则最小的电阻为$\frac{{c}^{2}R}{{a}^{2}}$.