题目内容
3.“辽宁号”航空母舰上舰载机的起飞问题一直备受关注.某学习小组的同学通过查阅资料对舰载机的起飞进行了模拟设计.如图,舰载机总质量为m,发动机额定功率为P,在水平轨道运行阶段所受阻力恒为f.舰载机在A处以额定功率启动,同时开启电磁弹射系统,它能额外给舰载机提供水平向右、大小为F的恒定推力.经历时间t1,舰载机运行至B处,速度达到v1,电磁弹射系统关闭.舰载机继续以额定功率加速运行至C处,经历的时间为t2,速度达到v2.此后,舰载机进入倾斜曲面轨道,在D处离开航母起飞.请根据以上信息求解下列问题.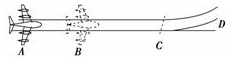
(1)电磁弹射系统关闭的瞬间舰载机的加速度;
(2)水平轨道AC的长度.
分析 (1)根据功率公式P=F1v1,求解出发动机的牵引力,根据牛顿第二定律求解加速度.
(2)舰载机在A处以额定功率启动,同时开启电磁弹射系统,它能额外给舰载机提供水平向右、大小为F的恒定推力.先根据动能定理研究BC段,列出方程;电磁弹射系统关闭.舰载机继续以额定功率加速运行至C处,再运用动能定理列式,联立即可求解AC的长度.
解答 解:(1)根据功率表达式可得:F1=$\frac{P}{{v}_{1}}$,
由牛顿第二运动定律得:F1-f=ma,解得:a=$\frac{P}{m{v}_{1}}$-$\frac{f}{m}$.
(2)舰载机在A处以额定功率启动,同时开启电磁弹射系统,
它能额外给舰载机提供水平向右、大小为F的恒定推力.经历时间t1,
舰载机运行至B处,速度达到v1,AB长度设为x1,由动能定理得:
Pt1+Fx1-fx1=$\frac{1}{2}$mv12,
电磁弹射系统关闭,舰载机继续以额定功率加速运行至C处,
经历的时间为t2,速度达到v2,BC长度设为x2.
由动能定理得:Pt2-fx2=$\frac{1}{2}$mv22-$\frac{1}{2}$mv12,
水平轨道的长度:AC=x1+x2,解得:AC=$\frac{\frac{1}{2}m{v}_{1}^{2}-P{t}_{1}}{F-f}$+$\frac{P{t}_{2}+\frac{1}{2}m{v}_{1}^{2}-\frac{1}{2}m{v}_{2}^{2}}{f}$;
答:(1)电磁弹射系统关闭的瞬间舰载机的加速度为$\frac{P}{m{v}_{1}}$-$\frac{f}{m}$;
(2)水平轨道AC的长度为$\frac{\frac{1}{2}m{v}_{1}^{2}-P{t}_{1}}{F-f}$+$\frac{P{t}_{2}+\frac{1}{2}m{v}_{1}^{2}-\frac{1}{2}m{v}_{2}^{2}}{f}$.
点评 灵活运用动能定理处理变力做功问题是解决本题的关键,运用时要灵活选取研究的过程,掌握功率一定时,W=Pt是求功的常用方法.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案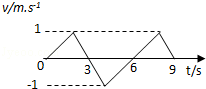
| A. | 往复运动 | B. | 加速度大小始终不变 | ||
| C. | 3s末速度为零 | D. | 6s末位移为零 |
| A. | 物体之间普遍存在相互吸引力 | |
| B. | 力不是维持物体运动的原因物体 | |
| C. | 忽略空气阻力,重物与轻物下落得同样快 | |
| D. | 物体间的相互作用力总是大小相等,方向相反 |
| A. | 11.5m/s | B. | 10.5m/s | C. | 10m/s | D. | 9.5m/s |
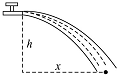 2010年3月22日是第18届“世界水日”,联合国确定的宣传主题是“清洁用水,健康用水”.我国是水资源严重缺乏的国家,节约用水是一项基本国策.土地浇灌时,由大水漫灌改为喷灌,能够节约很多淡水.如图所示的是推行节水工程的转动喷水“龙头”,“龙头”距地面高为h,它沿水平方向把水喷出的距离为x,设“水龙头”的直径为d,则此喷水“龙头”的流量为$\frac{πx{d}^{2}}{4}\sqrt{\frac{g}{2h}}$.
2010年3月22日是第18届“世界水日”,联合国确定的宣传主题是“清洁用水,健康用水”.我国是水资源严重缺乏的国家,节约用水是一项基本国策.土地浇灌时,由大水漫灌改为喷灌,能够节约很多淡水.如图所示的是推行节水工程的转动喷水“龙头”,“龙头”距地面高为h,它沿水平方向把水喷出的距离为x,设“水龙头”的直径为d,则此喷水“龙头”的流量为$\frac{πx{d}^{2}}{4}\sqrt{\frac{g}{2h}}$.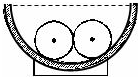 如图所示,两个质量均为0.4kg的光滑球,其半径均为r=3cm,将其放置在光滑半球形碗底,半球形碗口各处处于同一水平面上.两球最终在半径R=8cm的光滑半球形碗底稳定后处于静止状态,求两球之间相互作用力的大小(取g=10m/s2,sin 37°=0.6,cos 37°=0.8)
如图所示,两个质量均为0.4kg的光滑球,其半径均为r=3cm,将其放置在光滑半球形碗底,半球形碗口各处处于同一水平面上.两球最终在半径R=8cm的光滑半球形碗底稳定后处于静止状态,求两球之间相互作用力的大小(取g=10m/s2,sin 37°=0.6,cos 37°=0.8)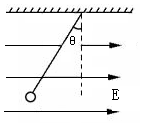 如图所示,一质量m=12g,带电荷量q=3.0×10-6C 的小球,用绝缘细线悬挂在水平向右的匀强电场中,静止时悬线向左与竖直方向成θ=37°角.
如图所示,一质量m=12g,带电荷量q=3.0×10-6C 的小球,用绝缘细线悬挂在水平向右的匀强电场中,静止时悬线向左与竖直方向成θ=37°角.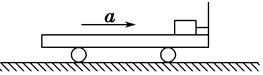 如图,一木块通过长度忽略不计的绳固定在小车的前壁上,小车上表面光滑.某时刻小车由静止开始向右匀加速运动,经过2s,细绳断裂.细绳断裂后,小车的加速度不变,又经过一段时间,滑块从小车左端刚好掉下,在这段时间内,滑块相对小车前3s内滑行了4.5m;后3s内滑行了10.5m.
如图,一木块通过长度忽略不计的绳固定在小车的前壁上,小车上表面光滑.某时刻小车由静止开始向右匀加速运动,经过2s,细绳断裂.细绳断裂后,小车的加速度不变,又经过一段时间,滑块从小车左端刚好掉下,在这段时间内,滑块相对小车前3s内滑行了4.5m;后3s内滑行了10.5m.