Question

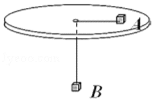
【题目】如图所示，圆盘中心有一个光滑小孔，用细绳穿过小孔，两端各系一物块A、B，A、B等质量，物块A与圆盘相对静止一起作匀速圆周运动，物块A匀速圆周运动的半径为r＝0.20m的匀速圆周运动：

(1)若圆盘光滑，要保持B物块静止，圆盘的角速度多大？

(2)若物块A与圆盘间的动摩擦因数为0.2，要保持B物块静止，圆盘的角速度的范围？取g＝10m/s2

Answer 1

【答案】(1)rad/s (2)2rad/s＜ω＜2rad/s

【解析】

(1)B保持静止，可知

T＝mg

对A分析，根据牛顿第二定律得

T＝mrω2

解得A的角速度

ω＝5rad/s

A和圆盘相对静止，故圆盘的角速度为5rad/s。

(2)物块A受到最大静摩擦力时，圆盘角速度存在极值。

当A所受最大静摩擦力与绳拉力方向相同时，合力提供向心力

mg+μmg＝mω12r

解得角速度

ω1＝2rad/s

同理，当A所受最大静摩擦力与绳的拉力方向相反时，合力提供向心力

mg﹣μmg＝mω22r

解得角速度

ω2＝2 rad/s

保持B物块静止，圆盘的角速度的取值范围为

2rad/s＜ω＜2rad/s。