Question

【题目】如图所示，两个相同的小球A、B用长度分别为l1、l2的细线（l1<l2）悬挂于天花板的O1、O2点，两球在水平面内做匀速圆周运动，两根细线与竖直轴夹角均为θ。设A、B两球的线速度分别为vA、vB，角速度分别为ωA、ωB，加速度分别为aA、aB，两根细线的拉力分别为FA、FB，则（ ）

A.FA<FB

B.vA>vB

C.aA=aB

D.ωA>ωB

Answer 1

【答案】CD

【解析】

A．小球在水平面内做匀速圆周运动，对小球受力分析，如图

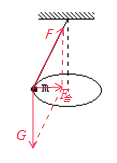
由几何关系可得细线的拉力为

由题知两个小球的质量相等，角度也相等，所以，故A错误；

B．由A项的受力分析，根据牛顿第二定律有

根据几何关系有

解得

由于，所以，故B错误；

C．根据牛顿第二定律有

解得

角度相等，故，故C正确；

D．根据

代入v、r的表达式解得

由于，所以，故D正确。

故选CD。