题目内容
7.比邻星是离太阳系最近(距离太阳4.2光年)的一颗恒星,据报道:2016年天文学家在比邻星的宜居带发现了一颗岩石行星-比邻星b;若比邻星b绕比邻星的公转半径是地球绕太阳的公转半径的p倍.比邻星b绕比邻星的公转周期是地球绕太阳的公转的q倍,则比邻星与太阳的质量比值为( )| A. | p3q2 | B. | p3q-2 | C. | p-3q2 | D. | p2q-3 |
分析 根据万有引力提供向心力分别求出比邻星和太阳的质量,从而得出比邻星质量是太阳质量的比值.
解答 解:根据$G\frac{{M}_{比邻}^{\;}{m}_{b}^{\;}}{{r}_{1}^{2}}={m}_{b}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{1}^{2}}{r}_{1}^{\;}$,得${M}_{比邻}^{\;}=\frac{4{π}_{\;}^{2}{r}_{1}^{3}}{G{T}_{1}^{2}}$.
根据$G\frac{{M}_{日}^{\;}{m}_{地}^{\;}}{{r}_{2}^{2}}={m}_{地}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{2}^{2}}{r}_{2}^{\;}$,解得${M}_{日}^{\;}=\frac{4{π}_{\;}^{2}{r}_{2}^{3}}{G{T}_{2}^{2}}$.
则$\frac{{M}_{比邻}^{\;}}{{M}_{日}^{\;}}=\frac{{r}_{1}^{3}}{{r}_{2}^{3}}•\frac{{T}_{2}^{2}}{{T}_{1}^{2}}={p}_{\;}^{3}•{q}_{\;}^{-2}$.故B正确,ACD错误;
故选:B
点评 环绕天体绕中心天体做圆周运动,通过万有引力提供向心力可以求出中心天体的质量,不能求出环绕天体的质量.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
15.下列说法中正确的是 ( )
| A. | 只有处于液态和气态的物体才能发生扩散现象 | |
| B. | 一定量的气体,从外界吸收热量2.7×105J,内能增加4.3×105J,则该过程中外界对气体做功1.6×105J | |
| C. | 动能大的物体比动能小的物体温度高 | |
| D. | 有无固定的熔点是区别晶体和非晶体的基础特征之一 | |
| E. | 气体压强就是大量气体分子作用在器壁单位面积上的平均作用力 |
19.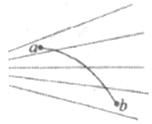 如图所示,实线是一带电粒子仅在电场力作用下由a点运动到b点的运动轨迹,虚线是电场线,则( )
如图所示,实线是一带电粒子仅在电场力作用下由a点运动到b点的运动轨迹,虚线是电场线,则( )
 如图所示,实线是一带电粒子仅在电场力作用下由a点运动到b点的运动轨迹,虚线是电场线,则( )
如图所示,实线是一带电粒子仅在电场力作用下由a点运动到b点的运动轨迹,虚线是电场线,则( )| A. | 粒子在a点的加速度一定小于在b点的加速度 | |
| B. | 粒子在a点的动能大于b点的动能 | |
| C. | 粒子在a点的电势能大于b点的电势能 | |
| D. | a点的电势一定高于b点的电势 |
15.以下关于玻尔原子理论的说法中正确的是( )
| A. | 电子绕原子核做圆周运动的轨逍半径可以取任意值 | |
| B. | 电子在绕原子核做圆周运动时,稳定地产生电磁辐射 | |
| C. | 电子从量子数为2的能级跃迁到量子数为3的能级时要辐射光子 | |
| D. | 不同频率的光照射处于基态的氢原子时,只有某些频率的光子可以被氢原子吸收 |

 ___________m/s;
___________m/s; _______m/s。
_______m/s。 。
。

 质量M=4kg的物块C以v=6m/s的速度在光滑的水平地面上向左运动,两物块A、B用轻弹簧相连,质量均为m=2kg,初始时弹簧处于原长,A、B两物块都静止在前方,如图所示,B与C碰撞后二者会粘在一起运动,求在以后的运动中.
质量M=4kg的物块C以v=6m/s的速度在光滑的水平地面上向左运动,两物块A、B用轻弹簧相连,质量均为m=2kg,初始时弹簧处于原长,A、B两物块都静止在前方,如图所示,B与C碰撞后二者会粘在一起运动,求在以后的运动中.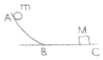 如图所示,光滑轨道的BC部分是水平的,质量为M的物体静置于轨道的BC部分,质量为m的物体从轨道上方的A点滑下,并与物体M发生无机械能损失的正碰,若要使m可与M发生第二次碰撞,$\frac{m}{M}$的比值不能超过多大?
如图所示,光滑轨道的BC部分是水平的,质量为M的物体静置于轨道的BC部分,质量为m的物体从轨道上方的A点滑下,并与物体M发生无机械能损失的正碰,若要使m可与M发生第二次碰撞,$\frac{m}{M}$的比值不能超过多大?