Question

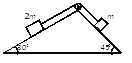
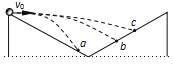
【题目】横截面为直角三角形的两个相同斜面紧靠在一起,固定在水平面上,如图所示。它们的竖直边长都是底边长的一半,现有三个小球从左边斜面的顶点以不同的初速度向右平抛,最后落在斜面上,其落点分别是a、b、c。若不计空气阻力,则下列判断正确的是( )

A. 三小球比较,落在c点的小球飞行过程速度变化最大

B. 三小球比较,落在c点的小球飞行过程速度变化最快

C. 三小球比较,落在c点的小球飞行时间最短

D. 无论小球抛出时初速度多大,落到斜面上的瞬时速度都不可能与斜面垂直

Answer 1

【答案】CD

【解析】A、小球在水平方向上保持恒定的初速度不变，速度变化为，落在a处的球的运动时间最长，即速度变化最大，故A错误；

B、3个小球的加速度都为重力加速度，故它们的速度变化一样快，故B错误；

C、3个小球都做平抛运动，竖直方向的下落高度为，可知落在C点的小球的下落高度最小，即飞行时间最短，故C正确；

D、落在左侧的斜面上的小球的瞬时速度不可能与斜面垂直；再进一步讨论b、c点，若瞬时速度的方向与斜面垂直，设斜面的倾角为，可得速度方向与竖直方向夹角为，，即，若要保证这个要求需满足，即水平位移的大小等于竖直位移，考虑三角形尺寸因素，知这种情况不成立，故D正确；

故选CD。