题目内容
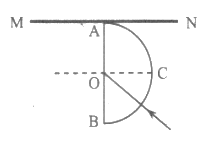
【题目】如图甲所示,竖直面MN的左侧空间中存在竖直向上的匀强电场(上、下及左侧无边界)。一个质量为![]() 、电荷量为
、电荷量为![]() 、可视为质点的带正电小球,以水平初速度
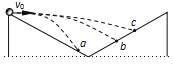
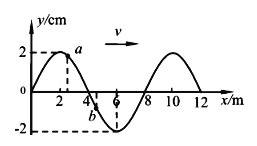
、可视为质点的带正电小球,以水平初速度![]() 沿PQ向右做直线运动。若小球刚经过D点时(t=0),在电场所在空间叠加如图乙所示随时间周期性变化、垂直纸面向里的匀强磁场,使得小球再次通过D点时与PQ连线成60°角。已知D、Q间的距离为(
沿PQ向右做直线运动。若小球刚经过D点时(t=0),在电场所在空间叠加如图乙所示随时间周期性变化、垂直纸面向里的匀强磁场,使得小球再次通过D点时与PQ连线成60°角。已知D、Q间的距离为(![]() +1)L,t0小于小球在磁场中做圆周运动的周期,忽略磁场变化造成的影响,重力加速度为g,求
+1)L,t0小于小球在磁场中做圆周运动的周期,忽略磁场变化造成的影响,重力加速度为g,求

(1)电场强度E的大小
(2)t0与t1的比值
(3)小球过D点后将做周期性运动, 则当小球运动的周期最大时,求出此时的磁感应强度的大小B0
及运动的最大周期Tm
【答案】(1)![]() (2)
(2) ![]()
【解析】(1)由平衡条件,有mg=Eq
解得E=![]()
(2)小球能再次通过D点,其运动轨迹如图所示,设半径为r,有s=v0t1

由几何关系得s=![]()
设小球做圆周运动的周期为T,则T=![]()
t0=![]() T
T
由以上四式得![]()
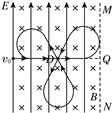
(3)当小球运动的周期最大时,其运动轨迹应与MN相切,小球运动一个周期的轨迹如图所示,由几何关系得
R+![]() =(
=(![]() +1)L
+1)L
由牛顿第二定律得qv0B0=m![]()
得 B0=![]()
小球在一个周期内运动的路程s1=3×![]() ×2πR+6×
×2πR+6×![]()
可得![]()

练习册系列答案
相关题目