Question

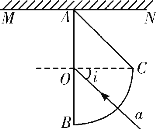
【题目】如图所示，光滑圆弧形凹槽ABC放在水平地面上，O为圆心，A、C两点等高且为圆弧边缘，B为最低点，张角∠AOC可随意调节，圆弧半径r=0．5m。现将OA与竖直方向的夹角θ1调为53°，把一个质量m=0．1kg的小球从水平桌面的边缘P点以v0=3m/s向右水平抛出，该小球恰能从A点沿圆弧的切线方向进入凹槽。已知sin53°=0．8，重力加速度g=10m/s2，不计空气阻力。

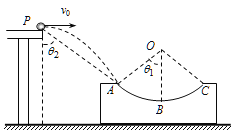
（1）求小球运动到A点时的速度大小；

（2）求小球在B点时对轨道的压力大小；

（3）改变θ1和v0的大小，同时把凹槽在水平地面上左右移动，使小球仍能从A点沿切线方向进入凹槽。若PA与竖直方向的夹角为θ2，试证明：。

Answer 1

【答案】（1）5m/s （2）6．8N（3）见解析；

【解析】

试题分析：（1）将小球经A点时的速度vA分解，有：

解得：

（2）小球从A到B的过程，由机械能守恒定律有

在B点，对小球有：

代入数据解得

由牛顿第三定律知，小球经B点时对圆槽的压力大小为6．8N。

（3）小球能从A点沿切线方向进入圆弧，说明其经A点时的速度vA与水平方向的夹角为θ1。设它从P到A的时间为t，则有：

所以有：，得证