题目内容
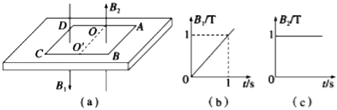
【题目】如图(a)所示为磁悬浮列车模型,质量M=1kg的绝缘板底座静止在动摩擦因数μ1=0.1的粗糙水平地面上.位于磁场中的正方形金属框ABCD为动力源,其质量m=1kg,边长为1m,电阻为![]() Ω.与绝缘板间的动摩擦因数μ2=0.4,OO′为AD、BC的中线.在金属框内有可随金属框同步移动的磁场,OO′CD区域内磁场如图(b)所示,CD恰在磁场边缘以外;OO′BA区域内磁场如图(c)所示,AB恰在磁场边缘以内(g=10m/s2).若绝缘板足够长且认为绝缘板与地面间最大静摩擦力等于滑动摩擦力.
Ω.与绝缘板间的动摩擦因数μ2=0.4,OO′为AD、BC的中线.在金属框内有可随金属框同步移动的磁场,OO′CD区域内磁场如图(b)所示,CD恰在磁场边缘以外;OO′BA区域内磁场如图(c)所示,AB恰在磁场边缘以内(g=10m/s2).若绝缘板足够长且认为绝缘板与地面间最大静摩擦力等于滑动摩擦力.
(1)若金属框固定在绝缘板上,则金属框从静止释放后,其整体加速度为多少?
(2)若金属框不固定,金属框的加速度又为多少?此时绝缘板是否静止,若不静止,其加速度又是多少?
【答案】(1)若金属框固定在绝缘板上,则金属框从静止释放后,其整体加速度为3 m/s2.
(2)若金属框不固定,金属框的加速度又为4 m/s2此时绝缘板不静止,其加速度又是2 m/s2
【解析】试题分析:(1)若金属框固定在绝缘板上,由题意得:
E=![]() SABCD=1××1×1 V="0.5" V,
SABCD=1××1×1 V="0.5" V,
则电流为:I=="8" A,
那么安培力为:FAB=B2IL="8" N,
取绝缘板和金属框整体进行受力分析,由牛顿第二定律有:
FAB﹣μ1(M+m)g=(M+m)a,
解得:a="3" m/s2.
(2)若金属框不固定,对金属框进行受力分析,假设其相对绝缘板滑动,有:
Ff1=μ2mg=0.4×1×10 N="4" N,
对金属框应用牛顿第二定律得:FAB﹣Ff1=ma1,a1="4" m/s2;
对绝缘板应用牛顿第二定律得:Ff1﹣Ff2=Ma2,Ff2=μ1(M+m)g="2" N,
解得:a2="2" m/s2,
a1>a2,假设正确.
金属框、绝缘板的加速度分别为4 m/s2、2 m/s2.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案