题目内容
【题目】一粗糙圆盘绕过盘心的竖直转轴在水平面内以角速度ω匀速转动,将质量m=1kg的滑块放在盘上距轴r=0.5m处随盘转动,滑块和转轴用拉长的轻质弹性绳连接。只有当盘的角速度满足2rad/s ≤ ω ≤ 4rad/s时,滑块才能相对盘静止。设最大静摩擦力等于滑动摩擦力,g取10m/s2,则:
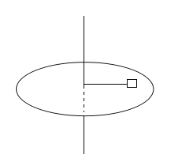
(1)滑块与盘间的动摩擦因数μ
(2)若当滑块和盘一起匀速转动时烧断弹性绳,滑块还能相对盘保持静止,求盘的角速度ω的取值范围
【答案】(1)0.3(2)![]()
【解析】
(1)当盘的角速度最小时,滑块受到的静摩擦力方向向外且达到最大,此时对滑块:![]()
当盘的角速度最大时,滑块受到的静摩擦力方向向里且达到最大,此时对滑块:![]()
解得μ=0.3
(2)若烧断弹性绳仍相对盘保持静止,则盘转动的角速度最大为ω3,此时滑块受的静摩擦力达到最大且方向指向圆心
![]()
解得![]()
则盘转动的角速度的范围:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目